Dmitry Yershov
Liability, Ethics, and Culture-Aware Behavior Specification using Rulebooks
Mar 01, 2019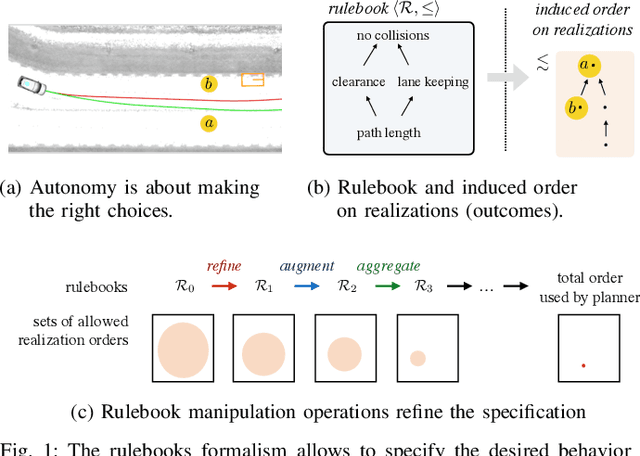
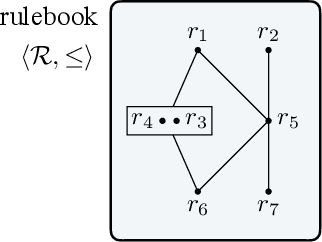
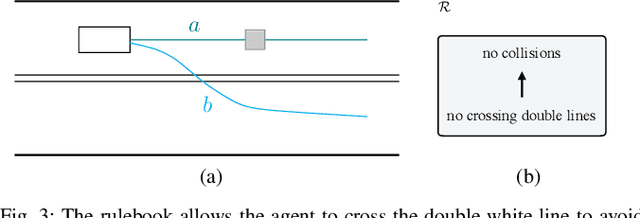
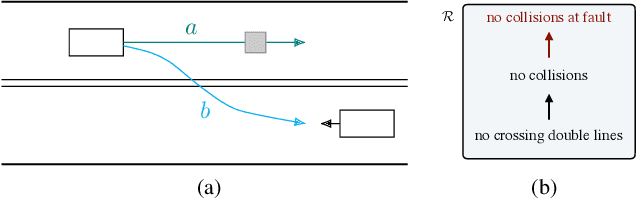
Abstract:The behavior of self-driving cars must be compatible with an enormous set of conflicting and ambiguous objectives, from law, from ethics, from the local culture, and so on. This paper describes a new way to conveniently define the desired behavior for autonomous agents, which we use on the self-driving cars developed at nuTonomy. We define a "rulebook" as a pre-ordered set of "rules", each akin to a violation metric on the possible outcomes ("realizations"). The rules are partially ordered by priority. The semantics of a rulebook imposes a pre-order on the set of realizations. We study the compositional properties of the rulebooks, and we derive which operations we can allow on the rulebooks to preserve previously-introduced constraints. While we demonstrate the application of these techniques in the self-driving domain, the methods are domain-independent.
Efficient Nearest-Neighbor Search for Dynamical Systems with Nonholonomic Constraints
Sep 22, 2017

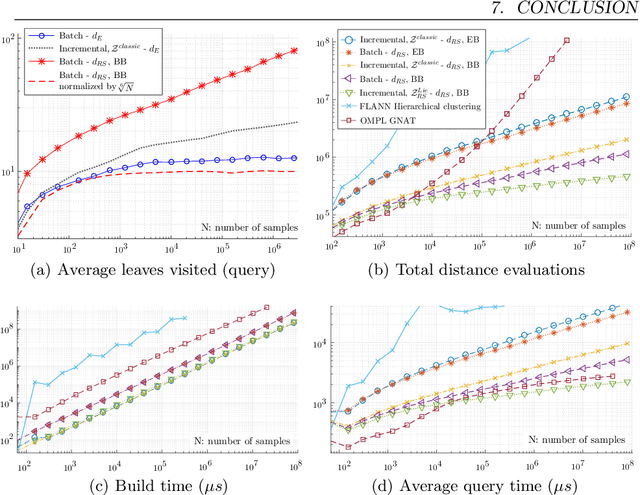
Abstract:Nearest-neighbor search dominates the asymptotic complexity of sampling-based motion planning algorithms and is often addressed with k-d tree data structures. While it is generally believed that the expected complexity of nearest-neighbor queries is $O(log(N))$ in the size of the tree, this paper reveals that when a classic k-d tree approach is used with sub-Riemannian metrics, the expected query complexity is in fact $\Theta(N^p \log(N))$ for a number $p \in [0, 1)$ determined by the degree of nonholonomy of the system. These metrics arise naturally in nonholonomic mechanical systems, including classic wheeled robot models. To address this negative result, we propose novel k-d tree build and query strategies tailored to sub-Riemannian metrics and demonstrate significant improvements in the running time of nearest-neighbor search queries.
A Survey of Motion Planning and Control Techniques for Self-driving Urban Vehicles
Apr 25, 2016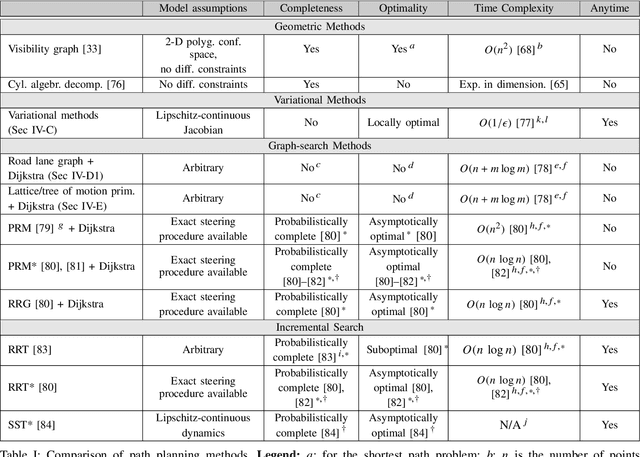
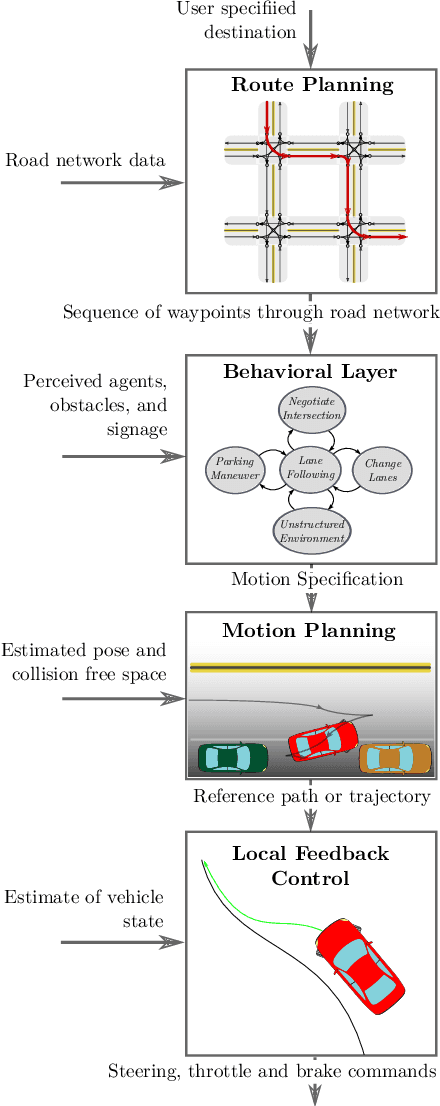


Abstract:Self-driving vehicles are a maturing technology with the potential to reshape mobility by enhancing the safety, accessibility, efficiency, and convenience of automotive transportation. Safety-critical tasks that must be executed by a self-driving vehicle include planning of motions through a dynamic environment shared with other vehicles and pedestrians, and their robust executions via feedback control. The objective of this paper is to survey the current state of the art on planning and control algorithms with particular regard to the urban setting. A selection of proposed techniques is reviewed along with a discussion of their effectiveness. The surveyed approaches differ in the vehicle mobility model used, in assumptions on the structure of the environment, and in computational requirements. The side-by-side comparison presented in this survey helps to gain insight into the strengths and limitations of the reviewed approaches and assists with system level design choices.
Planning for Optimal Feedback Control in the Volume of Free Space
Apr 29, 2015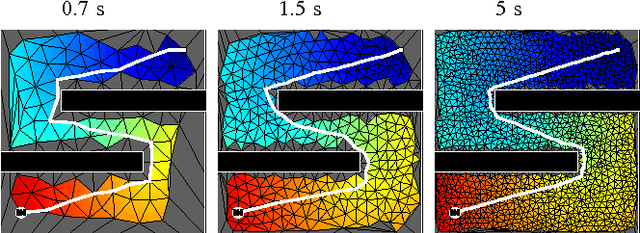

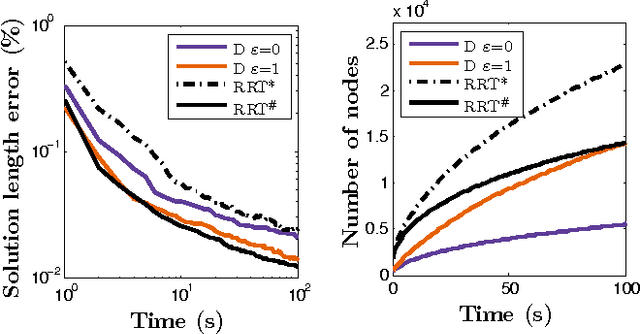
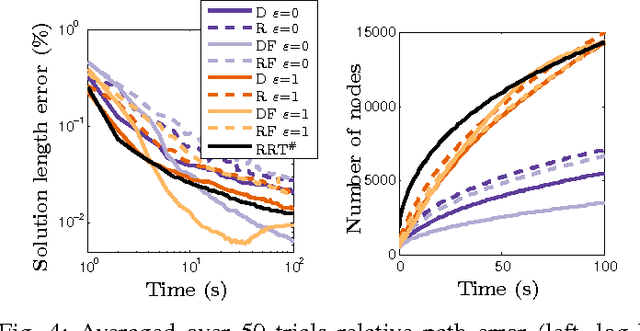
Abstract:The problem of optimal feedback planning among obstacles in d-dimensional configuration spaces is considered. We present a sampling-based, asymptotically optimal feedback planning method. Our method combines an incremental construction of the Delaunay triangulation, volumetric collision-detection module, and a modified Fast Marching Method to compute a converging sequence of feedback functions. The convergence and asymptotic runtime are proven theoretically and investigated during numerical experiments, in which the proposed method is compared with the state-of-the-art asymptotically optimal path planners. The results show that our method is competitive with the previous algorithms. Unlike the shortest trajectory computed by many path planning algorithms, the resulting feedback functions can be used directly for robot navigation in our case. Finally, we present a straightforward extension of our method that handles dynamic environments where obstacles can appear, disappear, or move.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge