Efficient Nearest-Neighbor Search for Dynamical Systems with Nonholonomic Constraints
Paper and Code
Sep 22, 2017

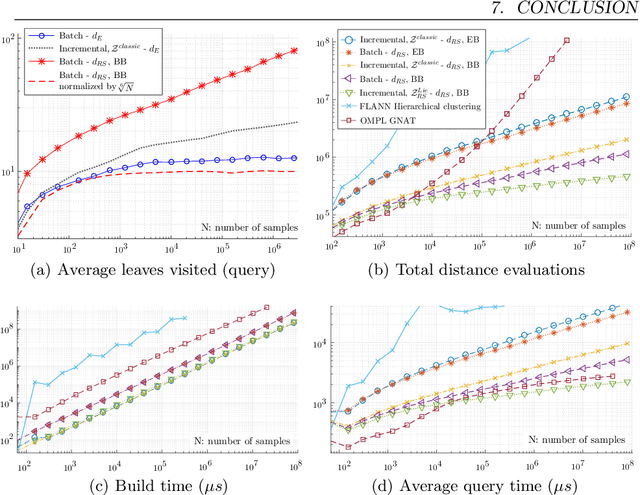
Nearest-neighbor search dominates the asymptotic complexity of sampling-based motion planning algorithms and is often addressed with k-d tree data structures. While it is generally believed that the expected complexity of nearest-neighbor queries is $O(log(N))$ in the size of the tree, this paper reveals that when a classic k-d tree approach is used with sub-Riemannian metrics, the expected query complexity is in fact $\Theta(N^p \log(N))$ for a number $p \in [0, 1)$ determined by the degree of nonholonomy of the system. These metrics arise naturally in nonholonomic mechanical systems, including classic wheeled robot models. To address this negative result, we propose novel k-d tree build and query strategies tailored to sub-Riemannian metrics and demonstrate significant improvements in the running time of nearest-neighbor search queries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge