Model predictive trajectory optimization and tracking for on-road autonomous vehicles

Motion planning for autonomous vehicles requires spatio-temporal motion plans (i.e. state trajectories) to account for dynamic obstacles. This requires a trajectory tracking control process which faithfully tracks planned trajectories. In this paper, a control scheme is presented which first optimizes a planned trajectory and then tracks the optimized trajectory using a feedback-feedforward controller. The feedforward element is calculated in a model predictive manner with a cost function focusing on driving performance. Stability of the error dynamic is then guaranteed by the design of the feedback-feedforward controller. The tracking performance of the control system is tested in a realistic simulated scenario where the control system must track an evasive lateral maneuver. The proposed controller performs well in simulation and can be easily adapted to different dynamic vehicle models. The uniqueness of the solution to the control synthesis eliminates any nondeterminism that could arise with switching between numerical solvers for the underlying mathematical program.

Efficient Nearest-Neighbor Search for Dynamical Systems with Nonholonomic Constraints

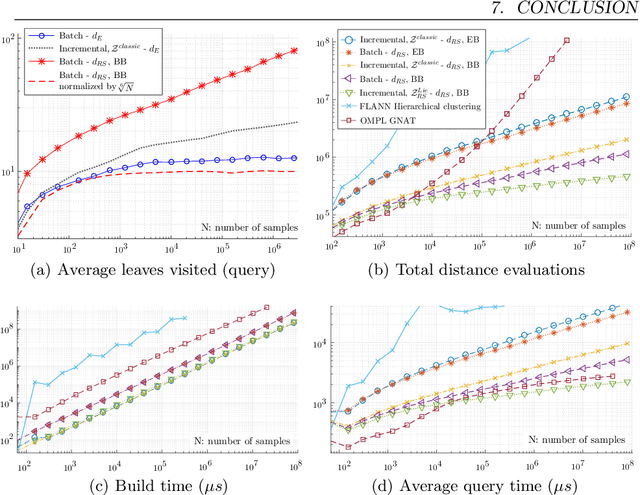
Nearest-neighbor search dominates the asymptotic complexity of sampling-based motion planning algorithms and is often addressed with k-d tree data structures. While it is generally believed that the expected complexity of nearest-neighbor queries is $O(log(N))$ in the size of the tree, this paper reveals that when a classic k-d tree approach is used with sub-Riemannian metrics, the expected query complexity is in fact $\Theta(N^p \log(N))$ for a number $p \in [0, 1)$ determined by the degree of nonholonomy of the system. These metrics arise naturally in nonholonomic mechanical systems, including classic wheeled robot models. To address this negative result, we propose novel k-d tree build and query strategies tailored to sub-Riemannian metrics and demonstrate significant improvements in the running time of nearest-neighbor search queries.

The Generalized Label Correcting Method for Optimal Kinodynamic Motion Planning

Nearly all autonomous robotic systems use some form of motion planning to compute reference motions through their environment. An increasing use of autonomous robots in a broad range of applications creates a need for efficient, general purpose motion planning algorithms that are applicable in any of these new application domains. This thesis presents a resolution complete optimal kinodynamic motion planning algorithm based on a direct forward search of the set of admissible input signals to a dynamical model. The advantage of this generalized label correcting method is that it does not require a local planning subroutine as in the case of related methods. Preliminary material focuses on new topological properties of the canonical problem formulation that are used to show continuity of the performance objective. These observations are used to derive a generalization of Bellman's principle of optimality in the context of kinodynamic motion planning. A generalized label correcting algorithm is then proposed which leverages these results to prune candidate input signals from the search when their cost is greater than related signals. The second part of this thesis addresses admissible heuristics for kinodynamic motion planning. An admissibility condition is derived that can be used to verify the admissibility of candidate heuristics for a particular problem. This condition also characterizes a convex set of admissible heuristics. A linear program is formulated to obtain a heuristic which is as close to the optimal cost-to-go as possible while remaining admissible. This optimization is justified by showing its solution coincides with the solution to the Hamilton-Jacobi-Bellman equation. Lastly, a sum-of-squares relaxation of this infinite-dimensional linear program is proposed for obtaining provably admissible approximate solutions.

Landmark Guided Probabilistic Roadmap Queries

A landmark based heuristic is investigated for reducing query phase run-time of the probabilistic roadmap (\PRM) motion planning method. The heuristic is generated by storing minimum spanning trees from a small number of vertices within the \PRM graph and using these trees to approximate the cost of a shortest path between any two vertices of the graph. The intermediate step of preprocessing the graph increases the time and memory requirements of the classical motion planning technique in exchange for speeding up individual queries making the method advantageous in multi-query applications. This paper investigates these trade-offs on \PRM graphs constructed in randomized environments as well as a practical manipulator simulation.We conclude that the method is preferable to Dijkstra's algorithm or the ${\rm A}^*$ algorithm with conventional heuristics in multi-query applications.

A Generalized Label Correcting Method for Optimal Kinodynamic Motion Planning

A resolution complete optimal kinodynamic motion planning algorithm is presented and described as a generalized label correcting (GLC) method. In contrast to related algorithms, the GLC method does not require a local planning subroutine and benefits from a simple implementation. The key contributions of this paper are the construction and analysis of the GLC conditions which are the basis of the proposed algorithm. Numerical experiments demonstrate the running time of the GLC method to be less than the related SST algorithm.

Design of Admissible Heuristics for Kinodynamic Motion Planning via Sum-of-Squares Programming

How does one obtain an admissible heuristic for a kinodynamic motion planning problem? This paper develops the analytical tools and techniques to answer this question. A sufficient condition for the admissibility of a heuristic is presented which can be checked directly from the problem data. This condition is also used to formulate a concave program to optimize an admissible heuristic. This optimization is then approximated and solved in polynomial time using sum-of-squares programming techniques. A number of examples are provided to demonstrate these concepts.

Selection of Input Primitives for the Generalized Label Correcting Method

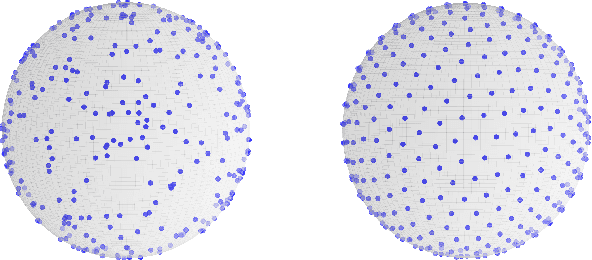
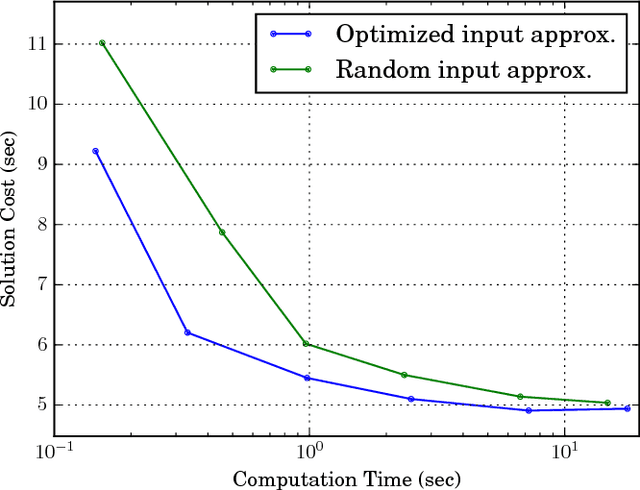
The generalized label correcting method is an efficient search-based approach to trajectory optimization. It relies on a finite set of control primitives that are concatenated into candidate control signals. This paper investigates the principled selection of this set of control primitives. Emphasis is placed on a particularly challenging input space geometry, the $n$-dimensional sphere. We propose using controls which minimize a generalized energy function and discuss the optimization technique used to obtain these control primitives. A numerical experiment is presented showing a factor of two improvement in running time when using the optimized control primitives over a random sampling strategy.

A Survey of Motion Planning and Control Techniques for Self-driving Urban Vehicles

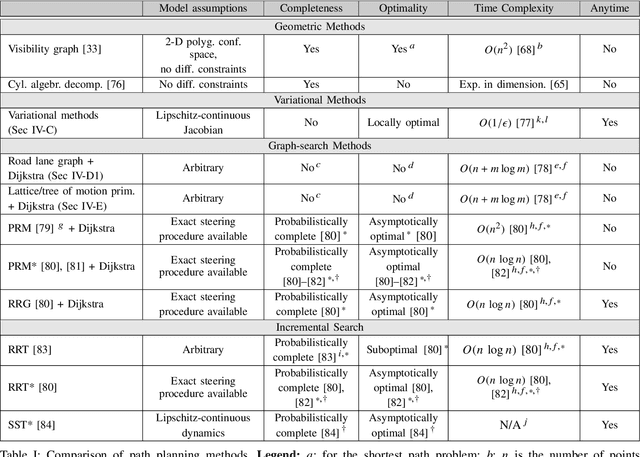
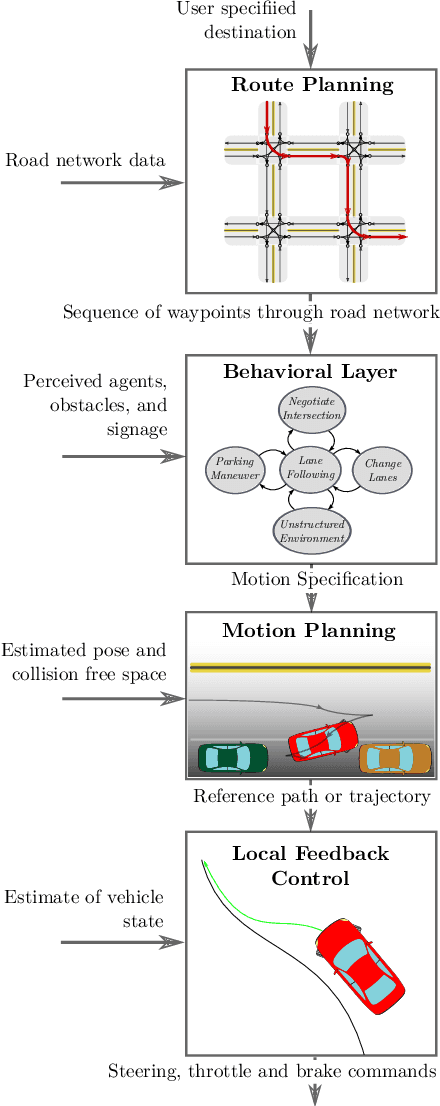
Self-driving vehicles are a maturing technology with the potential to reshape mobility by enhancing the safety, accessibility, efficiency, and convenience of automotive transportation. Safety-critical tasks that must be executed by a self-driving vehicle include planning of motions through a dynamic environment shared with other vehicles and pedestrians, and their robust executions via feedback control. The objective of this paper is to survey the current state of the art on planning and control algorithms with particular regard to the urban setting. A selection of proposed techniques is reviewed along with a discussion of their effectiveness. The surveyed approaches differ in the vehicle mobility model used, in assumptions on the structure of the environment, and in computational requirements. The side-by-side comparison presented in this survey helps to gain insight into the strengths and limitations of the reviewed approaches and assists with system level design choices.