Selection of Input Primitives for the Generalized Label Correcting Method
Paper and Code
Sep 20, 2016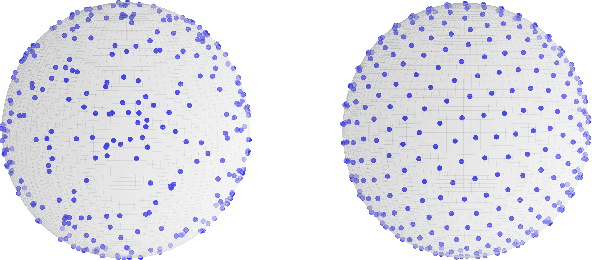

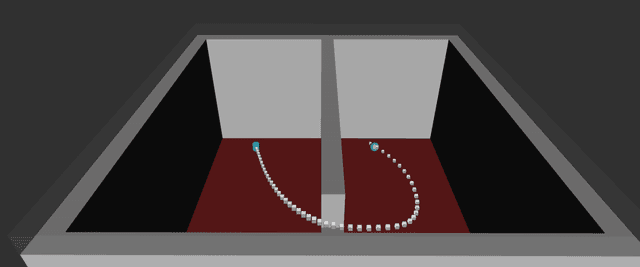
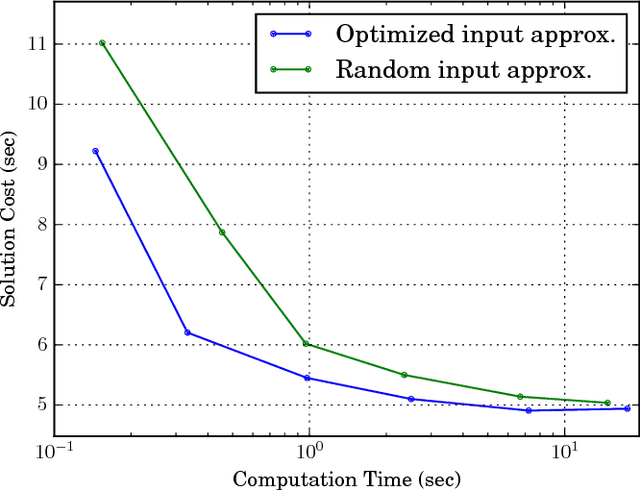
The generalized label correcting method is an efficient search-based approach to trajectory optimization. It relies on a finite set of control primitives that are concatenated into candidate control signals. This paper investigates the principled selection of this set of control primitives. Emphasis is placed on a particularly challenging input space geometry, the $n$-dimensional sphere. We propose using controls which minimize a generalized energy function and discuss the optimization technique used to obtain these control primitives. A numerical experiment is presented showing a factor of two improvement in running time when using the optimized control primitives over a random sampling strategy.
* 6 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge