Planning for Optimal Feedback Control in the Volume of Free Space
Paper and Code
Apr 29, 2015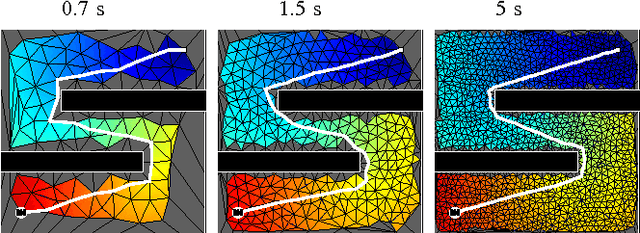

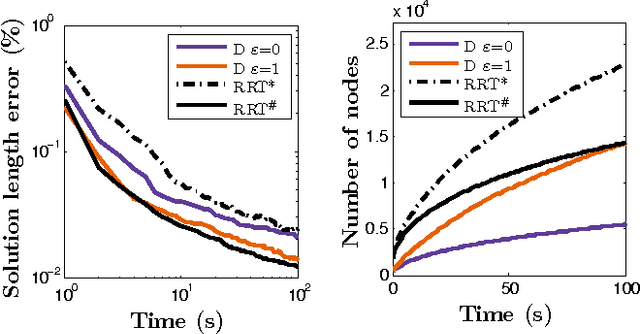
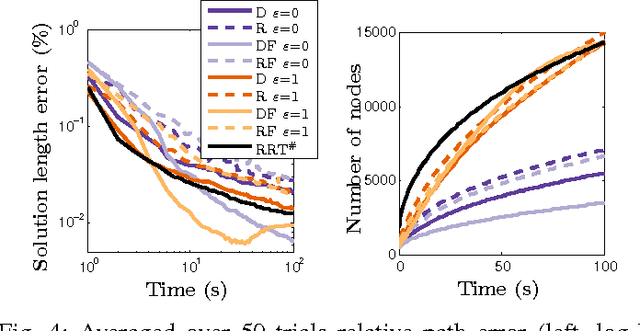
The problem of optimal feedback planning among obstacles in d-dimensional configuration spaces is considered. We present a sampling-based, asymptotically optimal feedback planning method. Our method combines an incremental construction of the Delaunay triangulation, volumetric collision-detection module, and a modified Fast Marching Method to compute a converging sequence of feedback functions. The convergence and asymptotic runtime are proven theoretically and investigated during numerical experiments, in which the proposed method is compared with the state-of-the-art asymptotically optimal path planners. The results show that our method is competitive with the previous algorithms. Unlike the shortest trajectory computed by many path planning algorithms, the resulting feedback functions can be used directly for robot navigation in our case. Finally, we present a straightforward extension of our method that handles dynamic environments where obstacles can appear, disappear, or move.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge