Preference-Optimized Pareto Set Learning for Blackbox Optimization

Multi-Objective Optimization (MOO) is an important problem in real-world applications. However, for a non-trivial problem, no single solution exists that can optimize all the objectives simultaneously. In a typical MOO problem, the goal is to find a set of optimum solutions (Pareto set) that trades off the preferences among objectives. Scalarization in MOO is a well-established method for finding a finite set approximation of the whole Pareto set (PS). However, in real-world experimental design scenarios, it's beneficial to obtain the whole PS for flexible exploration of the design space. Recently Pareto set learning (PSL) has been introduced to approximate the whole PS. PSL involves creating a manifold representing the Pareto front of a multi-objective optimization problem. A naive approach includes finding discrete points on the Pareto front through randomly generated preference vectors and connecting them by regression. However, this approach is computationally expensive and leads to a poor PS approximation. We propose to optimize the preference points to be distributed evenly on the Pareto front. Our formulation leads to a bilevel optimization problem that can be solved by e.g. differentiable cross-entropy methods. We demonstrated the efficacy of our method for complex and difficult black-box MOO problems using both synthetic and real-world benchmark data.

Molecule Graph Networks with Many-body Equivariant Interactions

Message passing neural networks have demonstrated significant efficacy in predicting molecular interactions. Introducing equivariant vectorial representations augments expressivity by capturing geometric data symmetries, thereby improving model accuracy. However, two-body bond vectors in opposition may cancel each other out during message passing, leading to the loss of directional information on their shared node. In this study, we develop Equivariant N-body Interaction Networks (ENINet) that explicitly integrates equivariant many-body interactions to preserve directional information in the message passing scheme. Experiments indicate that integrating many-body equivariant representations enhances prediction accuracy across diverse scalar and tensorial quantum chemical properties. Ablation studies show an average performance improvement of 7.9% across 11 out of 12 properties in QM9, 27.9% in forces in MD17, and 11.3% in polarizabilities (CCSD) in QM7b.

Feature Importance Measurement based on Decision Tree Sampling

Random forest is effective for prediction tasks but the randomness of tree generation hinders interpretability in feature importance analysis. To address this, we proposed DT-Sampler, a SAT-based method for measuring feature importance in tree-based model. Our method has fewer parameters than random forest and provides higher interpretability and stability for the analysis in real-world problems. An implementation of DT-Sampler is available at https://github.com/tsudalab/DT-sampler.

A Confidence Machine for Sparse High-Order Interaction Model

In predictive modeling for high-stake decision-making, predictors must be not only accurate but also reliable. Conformal prediction (CP) is a promising approach for obtaining the confidence of prediction results with fewer theoretical assumptions. To obtain the confidence set by so-called full-CP, we need to refit the predictor for all possible values of prediction results, which is only possible for simple predictors. For complex predictors such as random forests (RFs) or neural networks (NNs), split-CP is often employed where the data is split into two parts: one part for fitting and another to compute the confidence set. Unfortunately, because of the reduced sample size, split-CP is inferior to full-CP both in fitting as well as confidence set computation. In this paper, we develop a full-CP of sparse high-order interaction model (SHIM), which is sufficiently flexible as it can take into account high-order interactions among variables. We resolve the computational challenge for full-CP of SHIM by introducing a novel approach called homotopy mining. Through numerical experiments, we demonstrate that SHIM is as accurate as complex predictors such as RF and NN and enjoys the superior statistical power of full-CP.

Fast and More Powerful Selective Inference for Sparse High-order Interaction Model

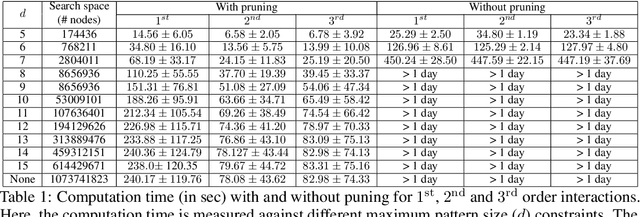
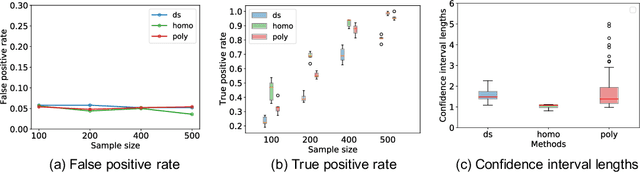
Automated high-stake decision-making such as medical diagnosis requires models with high interpretability and reliability. As one of the interpretable and reliable models with good prediction ability, we consider Sparse High-order Interaction Model (SHIM) in this study. However, finding statistically significant high-order interactions is challenging due to the intrinsic high dimensionality of the combinatorial effects. Another problem in data-driven modeling is the effect of "cherry-picking" a.k.a. selection bias. Our main contribution is to extend the recently developed parametric programming approach for selective inference to high-order interaction models. Exhaustive search over the cherry tree (all possible interactions) can be daunting and impractical even for a small-sized problem. We introduced an efficient pruning strategy and demonstrated the computational efficiency and statistical power of the proposed method using both synthetic and real data.