Dinesh Acharya
Sliced Wasserstein Generative Models
Apr 13, 2019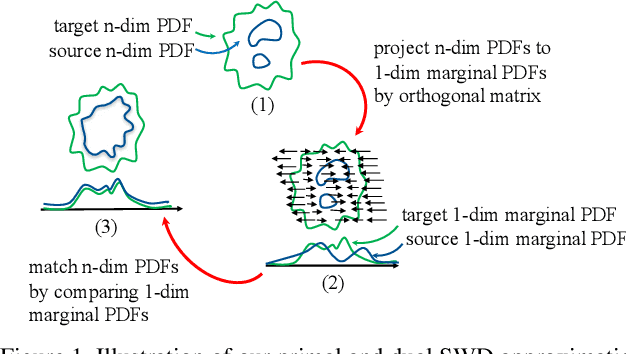
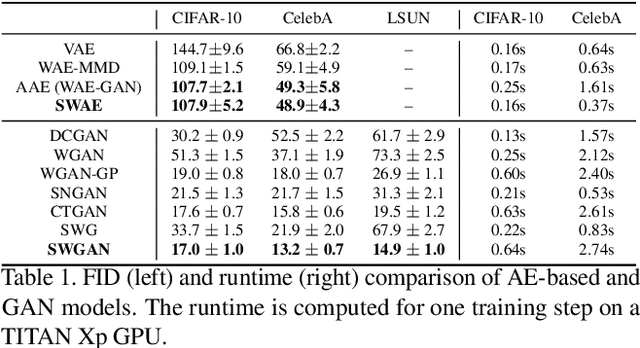
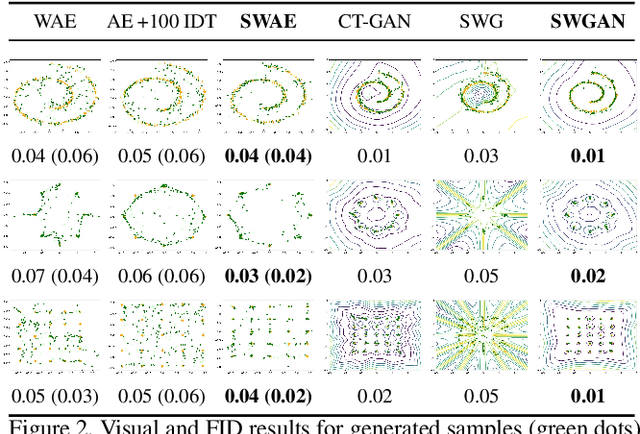
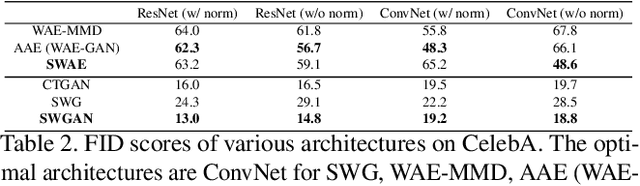
Abstract:In generative modeling, the Wasserstein distance (WD) has emerged as a useful metric to measure the discrepancy between generated and real data distributions. Unfortunately, it is challenging to approximate the WD of high-dimensional distributions. In contrast, the sliced Wasserstein distance (SWD) factorizes high-dimensional distributions into their multiple one-dimensional marginal distributions and is thus easier to approximate. In this paper, we introduce novel approximations of the primal and dual SWD. Instead of using a large number of random projections, as it is done by conventional SWD approximation methods, we propose to approximate SWDs with a small number of parameterized orthogonal projections in an end-to-end deep learning fashion. As concrete applications of our SWD approximations, we design two types of differentiable SWD blocks to equip modern generative frameworks---Auto-Encoders (AE) and Generative Adversarial Networks (GAN). In the experiments, we not only show the superiority of the proposed generative models on standard image synthesis benchmarks, but also demonstrate the state-of-the-art performance on challenging high resolution image and video generation in an unsupervised manner.
Wasserstein Divergence for GANs
Sep 05, 2018
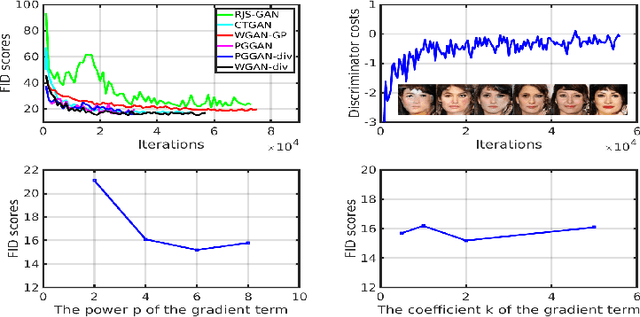
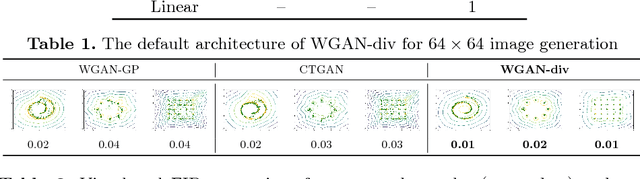

Abstract:In many domains of computer vision, generative adversarial networks (GANs) have achieved great success, among which the family of Wasserstein GANs (WGANs) is considered to be state-of-the-art due to the theoretical contributions and competitive qualitative performance. However, it is very challenging to approximate the $k$-Lipschitz constraint required by the Wasserstein-1 metric~(W-met). In this paper, we propose a novel Wasserstein divergence~(W-div), which is a relaxed version of W-met and does not require the $k$-Lipschitz constraint. As a concrete application, we introduce a Wasserstein divergence objective for GANs~(WGAN-div), which can faithfully approximate W-div through optimization. Under various settings, including progressive growing training, we demonstrate the stability of the proposed WGAN-div owing to its theoretical and practical advantages over WGANs. Also, we study the quantitative and visual performance of WGAN-div on standard image synthesis benchmarks of computer vision, showing the superior performance of WGAN-div compared to the state-of-the-art methods.
Covariance Pooling For Facial Expression Recognition
May 13, 2018



Abstract:Classifying facial expressions into different categories requires capturing regional distortions of facial landmarks. We believe that second-order statistics such as covariance is better able to capture such distortions in regional facial fea- tures. In this work, we explore the benefits of using a man- ifold network structure for covariance pooling to improve facial expression recognition. In particular, we first employ such kind of manifold networks in conjunction with tradi- tional convolutional networks for spatial pooling within in- dividual image feature maps in an end-to-end deep learning manner. By doing so, we are able to achieve a recognition accuracy of 58.14% on the validation set of Static Facial Expressions in the Wild (SFEW 2.0) and 87.0% on the vali- dation set of Real-World Affective Faces (RAF) Database. Both of these results are the best results we are aware of. Besides, we leverage covariance pooling to capture the tem- poral evolution of per-frame features for video-based facial expression recognition. Our reported results demonstrate the advantage of pooling image-set features temporally by stacking the designed manifold network of covariance pool-ing on top of convolutional network layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge