Sliced Wasserstein Generative Models
Paper and Code
Apr 13, 2019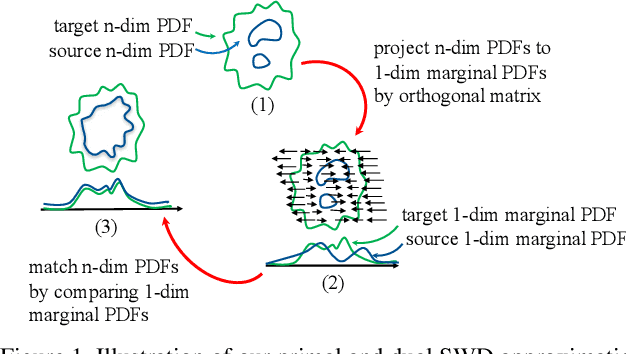
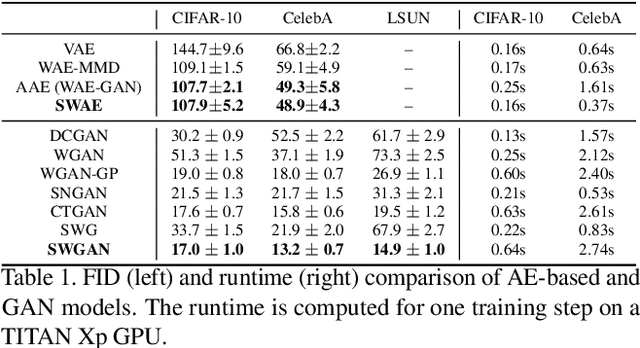
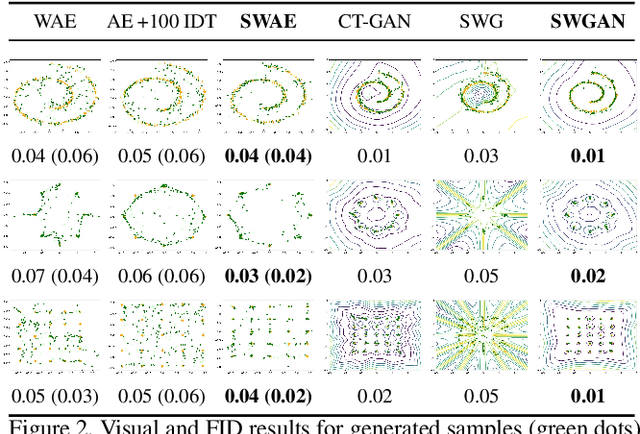
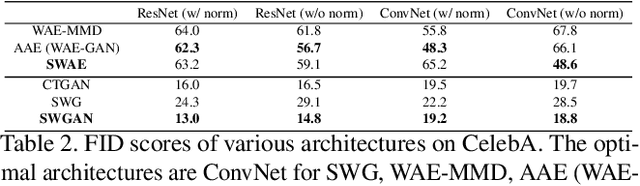
In generative modeling, the Wasserstein distance (WD) has emerged as a useful metric to measure the discrepancy between generated and real data distributions. Unfortunately, it is challenging to approximate the WD of high-dimensional distributions. In contrast, the sliced Wasserstein distance (SWD) factorizes high-dimensional distributions into their multiple one-dimensional marginal distributions and is thus easier to approximate. In this paper, we introduce novel approximations of the primal and dual SWD. Instead of using a large number of random projections, as it is done by conventional SWD approximation methods, we propose to approximate SWDs with a small number of parameterized orthogonal projections in an end-to-end deep learning fashion. As concrete applications of our SWD approximations, we design two types of differentiable SWD blocks to equip modern generative frameworks---Auto-Encoders (AE) and Generative Adversarial Networks (GAN). In the experiments, we not only show the superiority of the proposed generative models on standard image synthesis benchmarks, but also demonstrate the state-of-the-art performance on challenging high resolution image and video generation in an unsupervised manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge