Wasserstein Divergence for GANs
Paper and Code
Sep 05, 2018
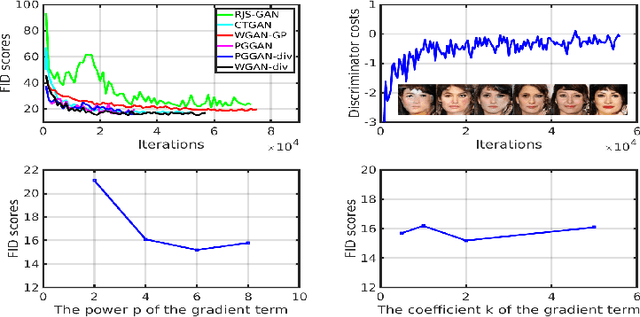
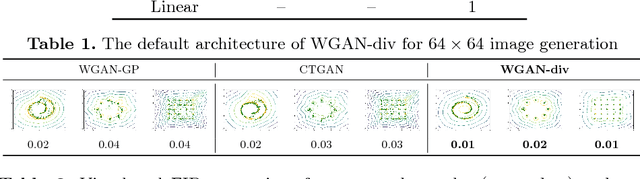

In many domains of computer vision, generative adversarial networks (GANs) have achieved great success, among which the family of Wasserstein GANs (WGANs) is considered to be state-of-the-art due to the theoretical contributions and competitive qualitative performance. However, it is very challenging to approximate the $k$-Lipschitz constraint required by the Wasserstein-1 metric~(W-met). In this paper, we propose a novel Wasserstein divergence~(W-div), which is a relaxed version of W-met and does not require the $k$-Lipschitz constraint. As a concrete application, we introduce a Wasserstein divergence objective for GANs~(WGAN-div), which can faithfully approximate W-div through optimization. Under various settings, including progressive growing training, we demonstrate the stability of the proposed WGAN-div owing to its theoretical and practical advantages over WGANs. Also, we study the quantitative and visual performance of WGAN-div on standard image synthesis benchmarks of computer vision, showing the superior performance of WGAN-div compared to the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge