Dimitri Bertsekas
Superior Computer Chess with Model Predictive Control, Reinforcement Learning, and Rollout
Sep 10, 2024Abstract:In this paper we apply model predictive control (MPC), rollout, and reinforcement learning (RL) methodologies to computer chess. We introduce a new architecture for move selection, within which available chess engines are used as components. One engine is used to provide position evaluations in an approximation in value space MPC/RL scheme, while a second engine is used as nominal opponent, to emulate or approximate the moves of the true opponent player. We show that our architecture improves substantially the performance of the position evaluation engine. In other words our architecture provides an additional layer of intelligence, on top of the intelligence of the engines on which it is based. This is true for any engine, regardless of its strength: top engines such as Stockfish and Komodo Dragon (of varying strengths), as well as weaker engines. Structurally, our basic architecture selects moves by a one-move lookahead search, with an intermediate move generated by a nominal opponent engine, and followed by a position evaluation by another chess engine. Simpler schemes that forego the use of the nominal opponent, also perform better than the position evaluator, but not quite by as much. More complex schemes, involving multistep lookahead, may also be used and generally tend to perform better as the length of the lookahead increases. Theoretically, our methodology relies on generic cost improvement properties and the superlinear convergence framework of Newton's method, which fundamentally underlies approximation in value space, and related MPC/RL and rollout/policy iteration schemes. A critical requirement of this framework is that the first lookahead step should be executed exactly. This fact has guided our architectural choices, and is apparently an important factor in improving the performance of even the best available chess engines.
An Approximate Dynamic Programming Framework for Occlusion-Robust Multi-Object Tracking
May 24, 2024Abstract:In this work, we consider data association problems involving multi-object tracking (MOT). In particular, we address the challenges arising from object occlusions. We propose a framework called approximate dynamic programming track (ADPTrack), which applies dynamic programming principles to improve an existing method called the base heuristic. Given a set of tracks and the next target frame, the base heuristic extends the tracks by matching them to the objects of this target frame directly. In contrast, ADPTrack first processes a few subsequent frames and applies the base heuristic starting from the next target frame to obtain tentative tracks. It then leverages the tentative tracks to match the objects of the target frame. This tends to reduce the occlusion-based errors and leads to an improvement over the base heuristic. When tested on the MOT17 video dataset, the proposed method demonstrates a 0.7% improvement in the association accuracy (IDF1 metric) over a state-of-the-art method that is used as the base heuristic. It also obtains improvements with respect to all the other standard metrics. Empirically, we found that the improvements are particularly pronounced in scenarios where the video data is obtained by fixed-position cameras.
Most Likely Sequence Generation for $n$-Grams, Transformers, HMMs, and Markov Chains, by Using Rollout Algorithms
Mar 19, 2024Abstract:In this paper we consider a transformer with an $n$-gram structure, such as the one underlying ChatGPT. The transformer provides next word probabilities, which can be used to generate word sequences. We consider methods for computing word sequences that are highly likely, based on these probabilities. Computing the optimal (i.e., most likely) word sequence starting with a given initial state is an intractable problem, so we propose methods to compute highly likely sequences of $N$ words in time that is a low order polynomial in $N$ and in the vocabulary size of the $n$-gram. These methods are based on the rollout approach from approximate dynamic programming, a form of single policy iteration, which can improve the performance of any given heuristic policy. In our case we use a greedy heuristic that generates as next word one that has the highest probability. We show with analysis, examples, and computational experimentation that our methods are capable of generating highly likely sequences with a modest increase in computation over the greedy heuristic. While our analysis and experiments are focused on Markov chains of the type arising in transformer and ChatGPT-like models, our methods apply to general finite-state Markov chains, and related inference applications of Hidden Markov Models (HMM), where Viterbi decoding is used extensively.
Approximate Multiagent Reinforcement Learning for On-Demand Urban Mobility Problem on a Large Map (extended version)
Nov 02, 2023
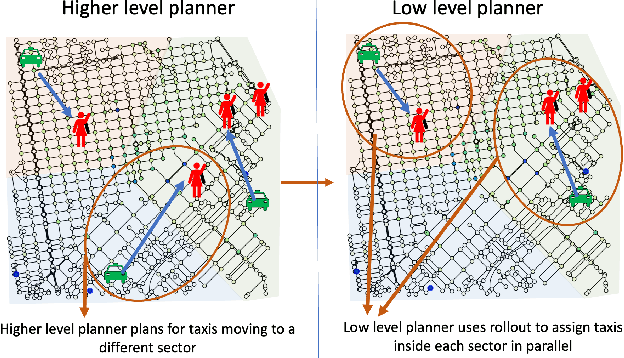
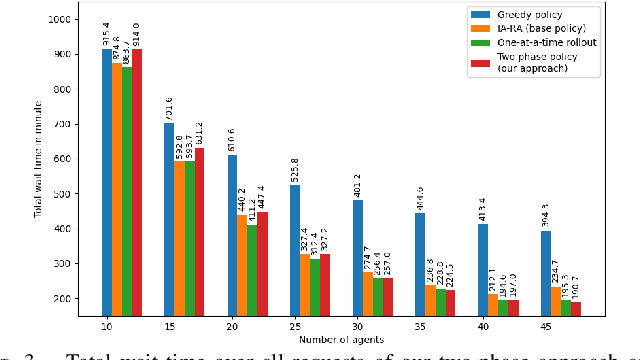
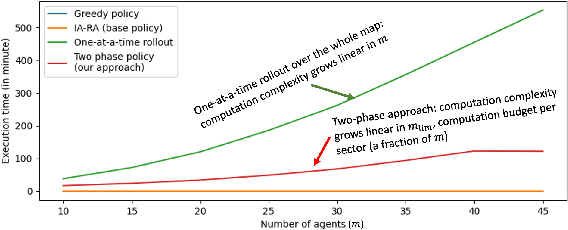
Abstract:In this paper, we focus on the autonomous multiagent taxi routing problem for a large urban environment where the location and number of future ride requests are unknown a-priori, but follow an estimated empirical distribution. Recent theory has shown that if a base policy is stable then a rollout-based algorithm with such a base policy produces a near-optimal stable policy. Although, rollout-based approaches are well-suited for learning cooperative multiagent policies with considerations for future demand, applying such methods to a large urban environment can be computationally expensive. Large environments tend to have a large volume of requests, and hence require a large fleet of taxis to guarantee stability. In this paper, we aim to address the computational bottleneck of multiagent (one-at-a-time) rollout, where the computational complexity grows linearly in the number of agents. We propose an approximate one-at-a-time rollout-based two-phase algorithm that reduces the computational cost, while still achieving a stable near-optimal policy. Our approach partitions the graph into sectors based on the predicted demand and an user-defined maximum number of agents that can be planned for using the one-at-a-time rollout approach. The algorithm then applies instantaneous assignment (IA) for re-balancing taxis across sectors and a sector-wide one-at-a-time rollout algorithm that is executed in parallel for each sector. We characterize the number of taxis $m$ that is sufficient for IA base policy to be stable, and derive a necessary condition on $m$ as time goes to infinity. Our numerical results show that our approach achieves stability for an $m$ that satisfies the theoretical conditions. We also empirically demonstrate that our proposed two-phase algorithm has comparable performance to the one-at-a-time rollout over the entire map, but with significantly lower runtimes.
Rollout Algorithms and Approximate Dynamic Programming for Bayesian Optimization and Sequential Estimation
Dec 29, 2022Abstract:We provide a unifying approximate dynamic programming framework that applies to a broad variety of problems involving sequential estimation. We consider first the construction of surrogate cost functions for the purposes of optimization, and we focus on the special case of Bayesian optimization, using the rollout algorithm and some of its variations. We then discuss the more general case of sequential estimation of a random vector using optimal measurement selection, and its application to problems of stochastic and adaptive control. We distinguish between adaptive control of deterministic and stochastic systems: the former are better suited for the use of rollout, while the latter are well suited for the use of rollout with certainty equivalence approximations. As an example of the deterministic case, we discuss sequential decoding problems, and a rollout algorithm for the approximate solution of the Wordle and Mastermind puzzles, recently developed in the paper [BBB22].
Reinforcement Learning Methods for Wordle: A POMDP/Adaptive Control Approach
Nov 29, 2022


Abstract:In this paper we address the solution of the popular Wordle puzzle, using new reinforcement learning methods, which apply more generally to adaptive control of dynamic systems and to classes of Partially Observable Markov Decision Process (POMDP) problems. These methods are based on approximation in value space and the rollout approach, admit a straightforward implementation, and provide improved performance over various heuristic approaches. For the Wordle puzzle, they yield on-line solution strategies that are very close to optimal at relatively modest computational cost. Our methods are viable for more complex versions of Wordle and related search problems, for which an optimal strategy would be impossible to compute. They are also applicable to a wide range of adaptive sequential decision problems that involve an unknown or frequently changing environment whose parameters are estimated on-line.
Multiagent Reinforcement Learning for Autonomous Routing and Pickup Problem with Adaptation to Variable Demand
Nov 28, 2022



Abstract:We derive a learning framework to generate routing/pickup policies for a fleet of vehicles tasked with servicing stochastically appearing requests on a city map. We focus on policies that 1) give rise to coordination amongst the vehicles, thereby reducing wait times for servicing requests, 2) are non-myopic, considering a-priori unknown potential future requests, and 3) can adapt to changes in the underlying demand distribution. Specifically, we are interested in adapting to fluctuations of actual demand conditions in urban environments, such as on-peak vs. off-peak hours. We achieve this through a combination of (i) online play, a lookahead optimization method that improves the performance of rollout methods via an approximate policy iteration step, and (ii) an offline approximation scheme that allows for adapting to changes in the underlying demand model. In particular, we achieve adaptivity of our learned policy to different demand distributions by quantifying a region of validity using the q-valid radius of a Wasserstein Ambiguity Set. We propose a mechanism for switching the originally trained offline approximation when the current demand is outside the original validity region. In this case, we propose to use an offline architecture, trained on a historical demand model that is closer to the current demand in terms of Wasserstein distance. We learn routing and pickup policies over real taxicab requests in downtown San Francisco with high variability between on-peak and off-peak hours, demonstrating the ability of our method to adapt to real fluctuation in demand distributions. Our numerical results demonstrate that our method outperforms rollout-based reinforcement learning, as well as several benchmarks based on classical methods from the field of operations research.
New Auction Algorithms for Path Planning, Network Transport, and Reinforcement Learning
Jul 19, 2022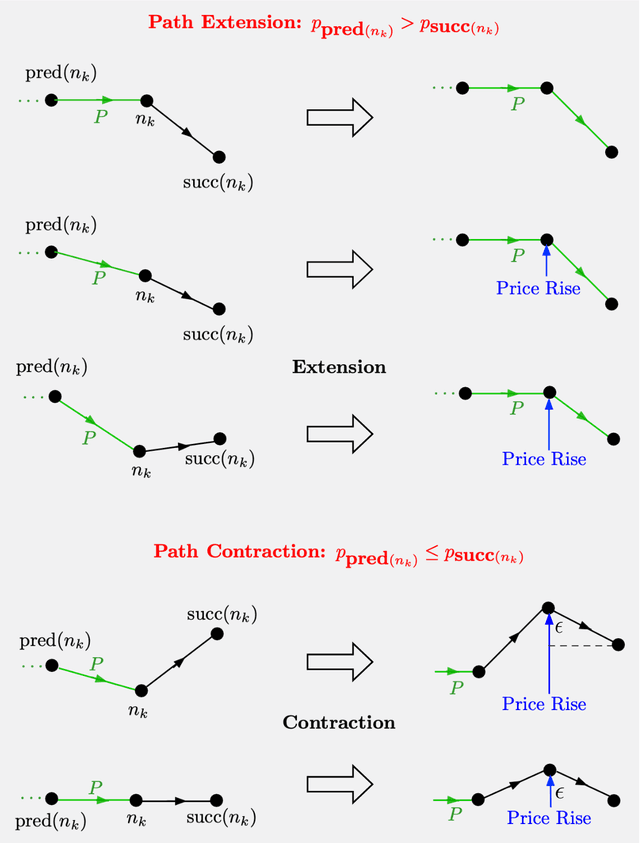
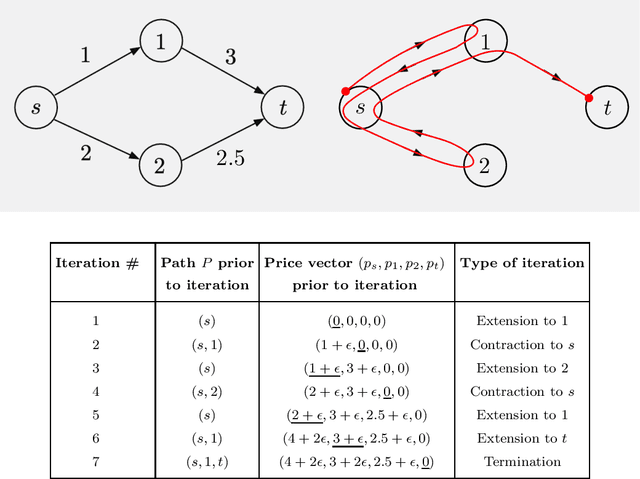
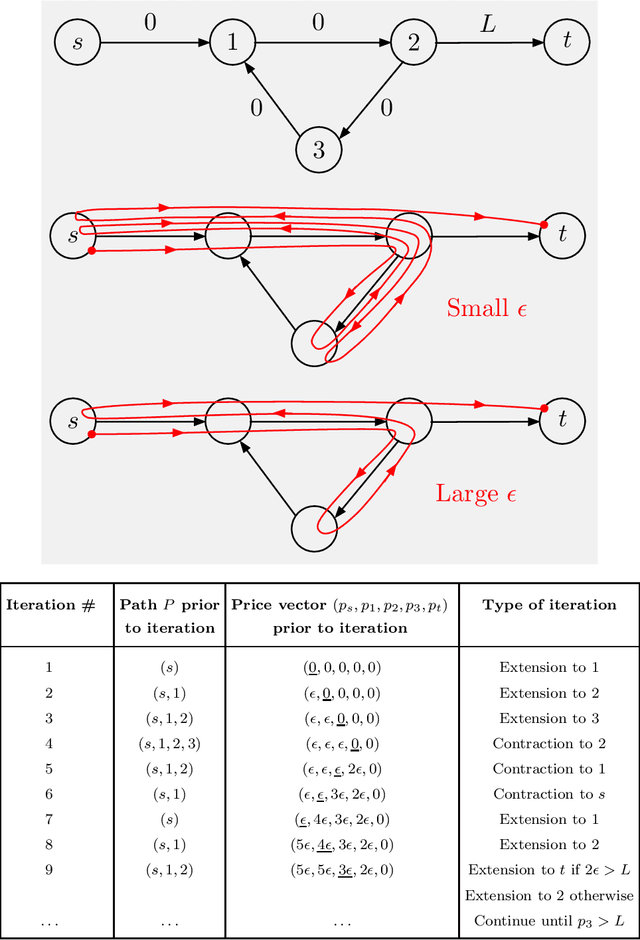
Abstract:We consider some classical optimization problems in path planning and network transport, and we introduce new auction-based algorithms for their optimal and suboptimal solution. The algorithms are based on mathematical ideas that are related to competitive bidding by persons for objects and the attendant market equilibrium, which underlie auction processes. However, the starting point of our algorithms is different, namely weighted and unweighted path construction in directed graphs, rather than assignment of persons to objects. The new algorithms have several potential advantages over existing methods: they are empirically faster in some important contexts, such as max-flow, they are well-suited for on-line replanning, and they can be adapted to distributed asynchronous operation. Moreover, they allow arbitrary initial prices, without complementary slackness restrictions, and thus are better-suited to take advantage of reinforcement learning methods that use off-line training with data, as well as on-line training during real-time operation. The new algorithms may also find use in reinforcement learning contexts involving approximation, such as multistep lookahead and tree search schemes, and/or rollout algorithms.
Lessons from AlphaZero for Optimal, Model Predictive, and Adaptive Control
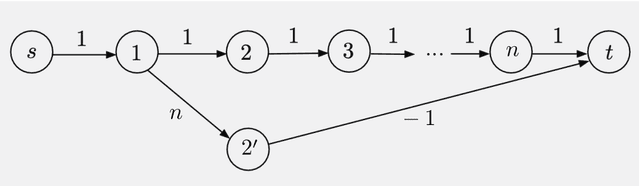
Aug 20, 2021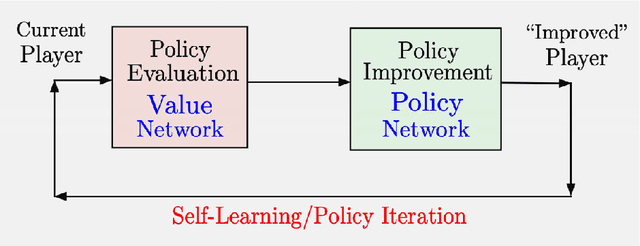
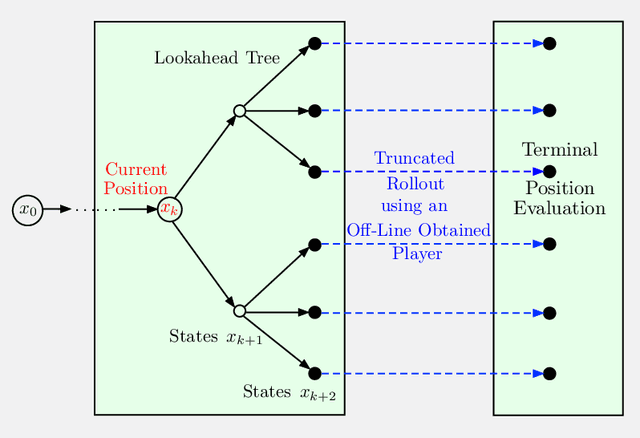
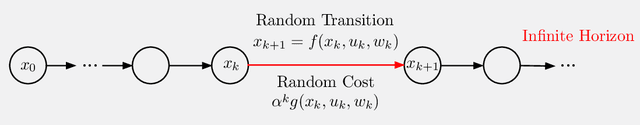
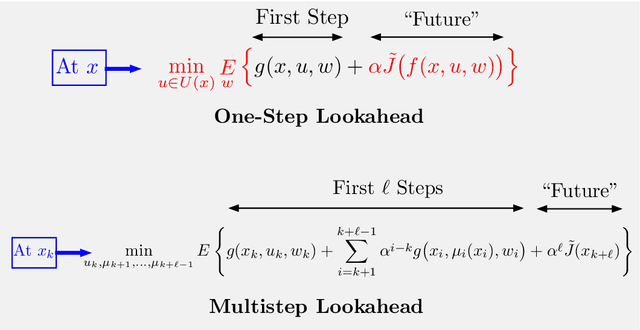
Abstract:In this paper we aim to provide analysis and insights (often based on visualization), which explain the beneficial effects of on-line decision making on top of off-line training. In particular, through a unifying abstract mathematical framework, we show that the principal AlphaZero/TD-Gammon ideas of approximation in value space and rollout apply very broadly to deterministic and stochastic optimal control problems, involving both discrete and continuous search spaces. Moreover, these ideas can be effectively integrated with other important methodologies such as model predictive control, adaptive control, decentralized control, discrete and Bayesian optimization, neural network-based value and policy approximations, and heuristic algorithms for discrete optimization.
On-Line Policy Iteration for Infinite Horizon Dynamic Programming
Jun 01, 2021Abstract:In this paper we propose an on-line policy iteration (PI) algorithm for finite-state infinite horizon discounted dynamic programming, whereby the policy improvement operation is done on-line, only for the states that are encountered during operation of the system. This allows the continuous updating/improvement of the current policy, thus resulting in a form of on-line PI that incorporates the improved controls into the current policy as new states and controls are generated. The algorithm converges in a finite number of stages to a type of locally optimal policy, and suggests the possibility of variants of PI and multiagent PI where the policy improvement is simplified. Moreover, the algorithm can be used with on-line replanning, and is also well-suited for on-line PI algorithms with value and policy approximations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge