Approximate Multiagent Reinforcement Learning for On-Demand Urban Mobility Problem on a Large Map (extended version)

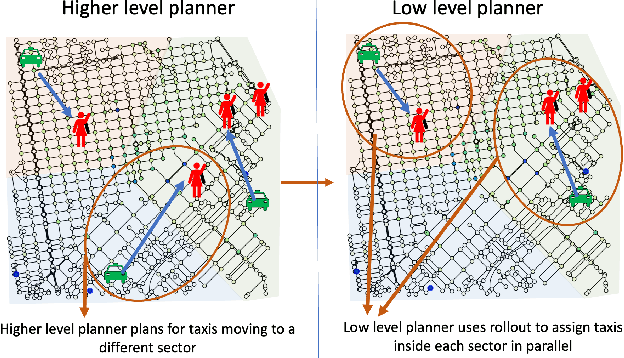
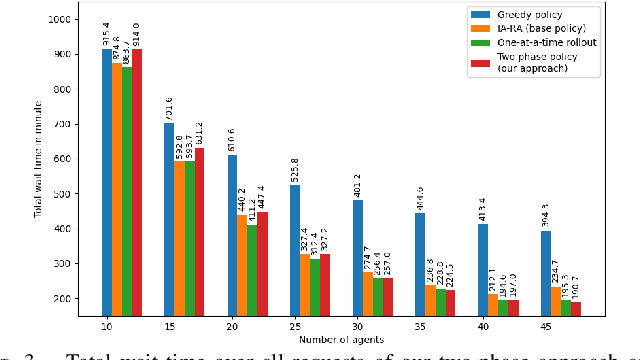
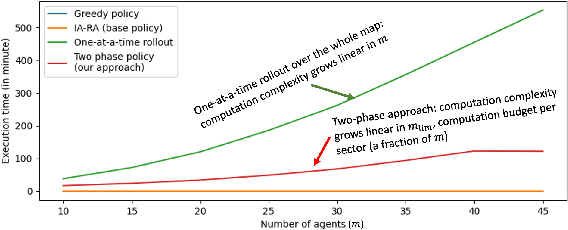
In this paper, we focus on the autonomous multiagent taxi routing problem for a large urban environment where the location and number of future ride requests are unknown a-priori, but follow an estimated empirical distribution. Recent theory has shown that if a base policy is stable then a rollout-based algorithm with such a base policy produces a near-optimal stable policy. Although, rollout-based approaches are well-suited for learning cooperative multiagent policies with considerations for future demand, applying such methods to a large urban environment can be computationally expensive. Large environments tend to have a large volume of requests, and hence require a large fleet of taxis to guarantee stability. In this paper, we aim to address the computational bottleneck of multiagent (one-at-a-time) rollout, where the computational complexity grows linearly in the number of agents. We propose an approximate one-at-a-time rollout-based two-phase algorithm that reduces the computational cost, while still achieving a stable near-optimal policy. Our approach partitions the graph into sectors based on the predicted demand and an user-defined maximum number of agents that can be planned for using the one-at-a-time rollout approach. The algorithm then applies instantaneous assignment (IA) for re-balancing taxis across sectors and a sector-wide one-at-a-time rollout algorithm that is executed in parallel for each sector. We characterize the number of taxis $m$ that is sufficient for IA base policy to be stable, and derive a necessary condition on $m$ as time goes to infinity. Our numerical results show that our approach achieves stability for an $m$ that satisfies the theoretical conditions. We also empirically demonstrate that our proposed two-phase algorithm has comparable performance to the one-at-a-time rollout over the entire map, but with significantly lower runtimes.

Multiagent Reinforcement Learning for Autonomous Routing and Pickup Problem with Adaptation to Variable Demand

We derive a learning framework to generate routing/pickup policies for a fleet of vehicles tasked with servicing stochastically appearing requests on a city map. We focus on policies that 1) give rise to coordination amongst the vehicles, thereby reducing wait times for servicing requests, 2) are non-myopic, considering a-priori unknown potential future requests, and 3) can adapt to changes in the underlying demand distribution. Specifically, we are interested in adapting to fluctuations of actual demand conditions in urban environments, such as on-peak vs. off-peak hours. We achieve this through a combination of (i) online play, a lookahead optimization method that improves the performance of rollout methods via an approximate policy iteration step, and (ii) an offline approximation scheme that allows for adapting to changes in the underlying demand model. In particular, we achieve adaptivity of our learned policy to different demand distributions by quantifying a region of validity using the q-valid radius of a Wasserstein Ambiguity Set. We propose a mechanism for switching the originally trained offline approximation when the current demand is outside the original validity region. In this case, we propose to use an offline architecture, trained on a historical demand model that is closer to the current demand in terms of Wasserstein distance. We learn routing and pickup policies over real taxicab requests in downtown San Francisco with high variability between on-peak and off-peak hours, demonstrating the ability of our method to adapt to real fluctuation in demand distributions. Our numerical results demonstrate that our method outperforms rollout-based reinforcement learning, as well as several benchmarks based on classical methods from the field of operations research.

Multiagent Rollout and Policy Iteration for POMDP with Application to Multi-Robot Repair Problems

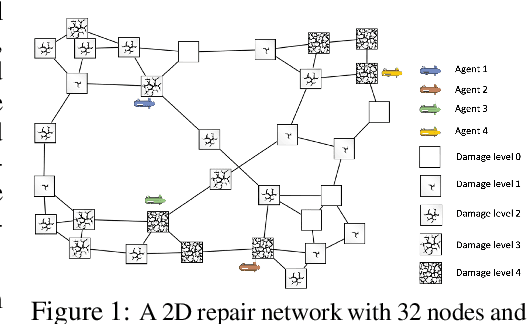
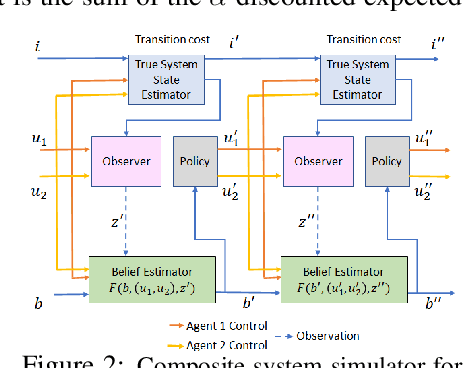
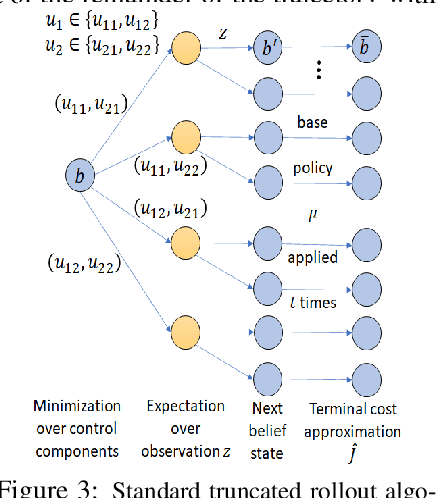
In this paper we consider infinite horizon discounted dynamic programming problems with finite state and control spaces, partial state observations, and a multiagent structure. We discuss and compare algorithms that simultaneously or sequentially optimize the agents' controls by using multistep lookahead, truncated rollout with a known base policy, and a terminal cost function approximation. Our methods specifically address the computational challenges of partially observable multiagent problems. In particular: 1) We consider rollout algorithms that dramatically reduce required computation while preserving the key cost improvement property of the standard rollout method. The per-step computational requirements for our methods are on the order of $O(Cm)$ as compared with $O(C^m)$ for standard rollout, where $C$ is the maximum cardinality of the constraint set for the control component of each agent, and $m$ is the number of agents. 2) We show that our methods can be applied to challenging problems with a graph structure, including a class of robot repair problems whereby multiple robots collaboratively inspect and repair a system under partial information. 3) We provide a simulation study that compares our methods with existing methods, and demonstrate that our methods can handle larger and more complex partially observable multiagent problems (state space size $10^{37}$ and control space size $10^{7}$, respectively). Finally, we incorporate our multiagent rollout algorithms as building blocks in an approximate policy iteration scheme, where successive rollout policies are approximated by using neural network classifiers. While this scheme requires a strictly off-line implementation, it works well in our computational experiments and produces additional significant performance improvement over the single online rollout iteration method.

Reinforcement Learning for POMDP: Partitioned Rollout and Policy Iteration with Application to Autonomous Sequential Repair Problems

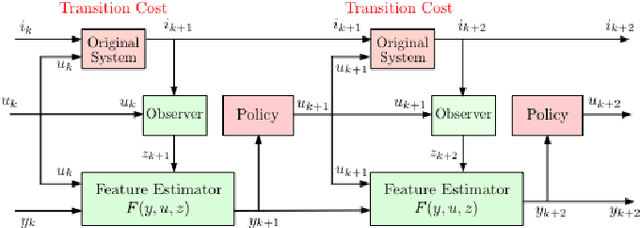
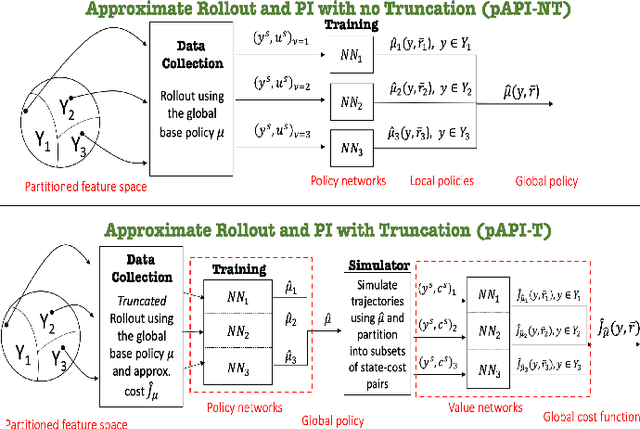
In this paper we consider infinite horizon discounted dynamic programming problems with finite state and control spaces, and partial state observations. We discuss an algorithm that uses multistep lookahead, truncated rollout with a known base policy, and a terminal cost function approximation. This algorithm is also used for policy improvement in an approximate policy iteration scheme, where successive policies are approximated by using a neural network classifier. A novel feature of our approach is that it is well suited for distributed computation through an extended belief space formulation and the use of a partitioned architecture, which is trained with multiple neural networks. We apply our methods in simulation to a class of sequential repair problems where a robot inspects and repairs a pipeline with potentially several rupture sites under partial information about the state of the pipeline.