Approximate Multiagent Reinforcement Learning for On-Demand Urban Mobility Problem on a Large Map (extended version)
Paper and Code
Nov 02, 2023
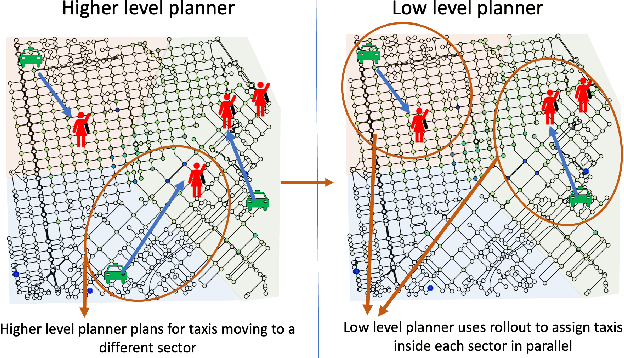
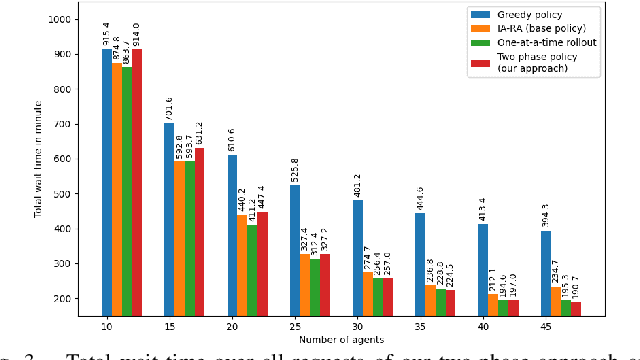
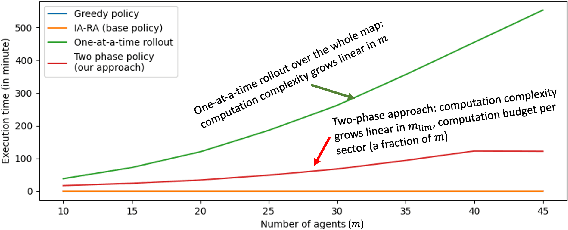
In this paper, we focus on the autonomous multiagent taxi routing problem for a large urban environment where the location and number of future ride requests are unknown a-priori, but follow an estimated empirical distribution. Recent theory has shown that if a base policy is stable then a rollout-based algorithm with such a base policy produces a near-optimal stable policy. Although, rollout-based approaches are well-suited for learning cooperative multiagent policies with considerations for future demand, applying such methods to a large urban environment can be computationally expensive. Large environments tend to have a large volume of requests, and hence require a large fleet of taxis to guarantee stability. In this paper, we aim to address the computational bottleneck of multiagent (one-at-a-time) rollout, where the computational complexity grows linearly in the number of agents. We propose an approximate one-at-a-time rollout-based two-phase algorithm that reduces the computational cost, while still achieving a stable near-optimal policy. Our approach partitions the graph into sectors based on the predicted demand and an user-defined maximum number of agents that can be planned for using the one-at-a-time rollout approach. The algorithm then applies instantaneous assignment (IA) for re-balancing taxis across sectors and a sector-wide one-at-a-time rollout algorithm that is executed in parallel for each sector. We characterize the number of taxis $m$ that is sufficient for IA base policy to be stable, and derive a necessary condition on $m$ as time goes to infinity. Our numerical results show that our approach achieves stability for an $m$ that satisfies the theoretical conditions. We also empirically demonstrate that our proposed two-phase algorithm has comparable performance to the one-at-a-time rollout over the entire map, but with significantly lower runtimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge