New Auction Algorithms for Path Planning, Network Transport, and Reinforcement Learning
Paper and Code
Jul 19, 2022
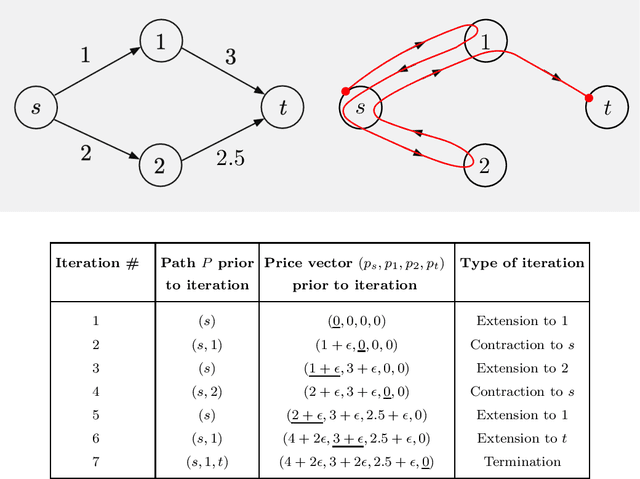
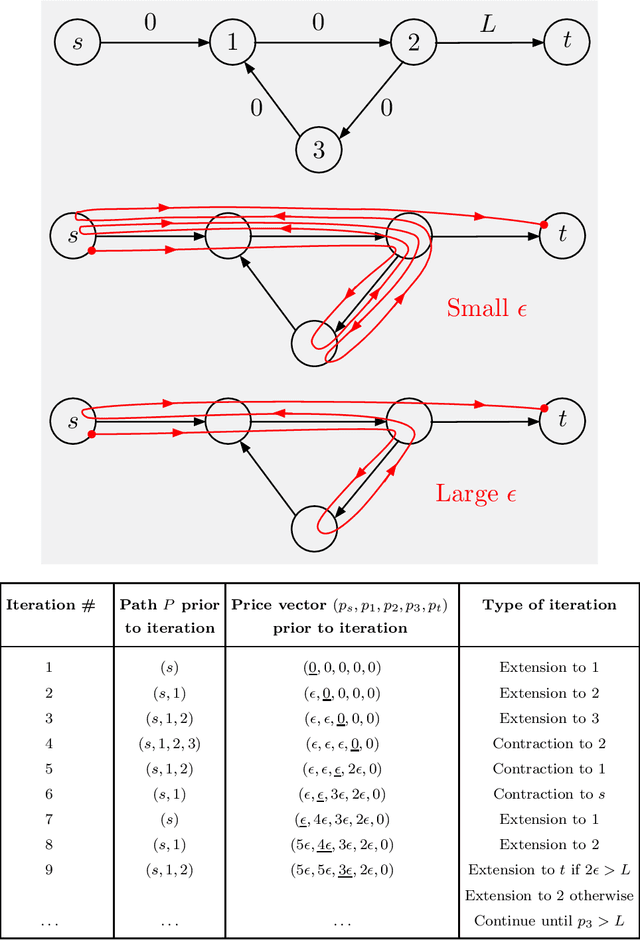
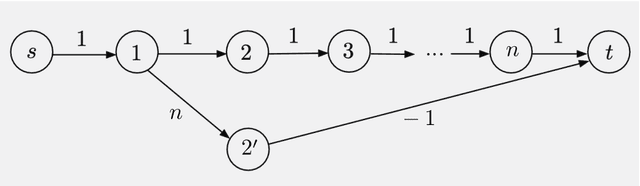
We consider some classical optimization problems in path planning and network transport, and we introduce new auction-based algorithms for their optimal and suboptimal solution. The algorithms are based on mathematical ideas that are related to competitive bidding by persons for objects and the attendant market equilibrium, which underlie auction processes. However, the starting point of our algorithms is different, namely weighted and unweighted path construction in directed graphs, rather than assignment of persons to objects. The new algorithms have several potential advantages over existing methods: they are empirically faster in some important contexts, such as max-flow, they are well-suited for on-line replanning, and they can be adapted to distributed asynchronous operation. Moreover, they allow arbitrary initial prices, without complementary slackness restrictions, and thus are better-suited to take advantage of reinforcement learning methods that use off-line training with data, as well as on-line training during real-time operation. The new algorithms may also find use in reinforcement learning contexts involving approximation, such as multistep lookahead and tree search schemes, and/or rollout algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge