Transforming Behavioral Neuroscience Discovery with In-Context Learning and AI-Enhanced Tensor Methods

Scientific discovery pipelines typically involve complex, rigid, and time-consuming processes, from data preparation to analyzing and interpreting findings. Recent advances in AI have the potential to transform such pipelines in a way that domain experts can focus on interpreting and understanding findings, rather than debugging rigid pipelines or manually annotating data. As part of an active collaboration between data science/AI researchers and behavioral neuroscientists, we showcase an example AI-enhanced pipeline, specifically designed to transform and accelerate the way that the domain experts in the team are able to gain insights out of experimental data. The application at hand is in the domain of behavioral neuroscience, studying fear generalization in mice, an important problem whose progress can advance our understanding of clinically significant and often debilitating conditions such as PTSD (Post-Traumatic Stress Disorder). We identify the emerging paradigm of "In-Context Learning" (ICL) as a suitable interface for domain experts to automate parts of their pipeline without the need for or familiarity with AI model training and fine-tuning, and showcase its remarkable efficacy in data preparation and pattern interpretation. Also, we introduce novel AI-enhancements to tensor decomposition model, which allows for more seamless pattern discovery from the heterogeneous data in our application. We thoroughly evaluate our proposed pipeline experimentally, showcasing its superior performance compared to what is standard practice in the domain, as well as against reasonable ML baselines that do not fall under the ICL paradigm, to ensure that we are not compromising performance in our quest for a seamless and easy-to-use interface for domain experts. Finally, we demonstrate effective discovery, with results validated by the domain experts in the team.

Extracting and Analyzing Rail Crossing Behavior Signatures from Videos using Tensor Methods

Railway crossings present complex safety challenges where driver behavior varies by location, time, and conditions. Traditional approaches analyze crossings individually, limiting the ability to identify shared behavioral patterns across locations. We propose a multi-view tensor decomposition framework that captures behavioral similarities across three temporal phases: Approach (warning activation to gate lowering), Waiting (gates down to train passage), and Clearance (train passage to gate raising). We analyze railway crossing videos from multiple locations using TimeSformer embeddings to represent each phase. By constructing phase-specific similarity matrices and applying non-negative symmetric CP decomposition, we discover latent behavioral components with distinct temporal signatures. Our tensor analysis reveals that crossing location appears to be a stronger determinant of behavior patterns than time of day, and that approach-phase behavior provides particularly discriminative signatures. Visualization of the learned component space confirms location-based clustering, with certain crossings forming distinct behavioral clusters. This automated framework enables scalable pattern discovery across multiple crossings, providing a foundation for grouping locations by behavioral similarity to inform targeted safety interventions.

Multi-view Graph Condensation via Tensor Decomposition

Graph Neural Networks (GNNs) have demonstrated remarkable results in various real-world applications, including drug discovery, object detection, social media analysis, recommender systems, and text classification. In contrast to their vast potential, training them on large-scale graphs presents significant computational challenges due to the resources required for their storage and processing. Graph Condensation has emerged as a promising solution to reduce these demands by learning a synthetic compact graph that preserves the essential information of the original one while maintaining the GNN's predictive performance. Despite their efficacy, current graph condensation approaches frequently rely on a computationally intensive bi-level optimization. Moreover, they fail to maintain a mapping between synthetic and original nodes, limiting the interpretability of the model's decisions. In this sense, a wide range of decomposition techniques have been applied to learn linear or multi-linear functions from graph data, offering a more transparent and less resource-intensive alternative. However, their applicability to graph condensation remains unexplored. This paper addresses this gap and proposes a novel method called Multi-view Graph Condensation via Tensor Decomposition (GCTD) to investigate to what extent such techniques can synthesize an informative smaller graph and achieve comparable downstream task performance. Extensive experiments on six real-world datasets demonstrate that GCTD effectively reduces graph size while preserving GNN performance, achieving up to a 4.0\ improvement in accuracy on three out of six datasets and competitive performance on large graphs compared to existing approaches. Our code is available at https://anonymous.4open.science/r/gctd-345A.

Improving Group Fairness in Tensor Completion via Imbalance Mitigating Entity Augmentation

Group fairness is important to consider in tensor decomposition to prevent discrimination based on social grounds such as gender or age. Although few works have studied group fairness in tensor decomposition, they suffer from performance degradation. To address this, we propose STAFF(Sparse Tensor Augmentation For Fairness) to improve group fairness by minimizing the gap in completion errors of different groups while reducing the overall tensor completion error. Our main idea is to augment a tensor with augmented entities including sufficient observed entries to mitigate imbalance and group bias in the sparse tensor. We evaluate \method on tensor completion with various datasets under conventional and deep learning-based tensor models. STAFF consistently shows the best trade-off between completion error and group fairness; at most, it yields 36% lower MSE and 59% lower MADE than the second-best baseline.

Global and Local Structure Learning for Sparse Tensor Completion

How can we accurately complete tensors by learning relationships of dimensions along each mode? Tensor completion, a widely studied problem, is to predict missing entries in incomplete tensors. Tensor decomposition methods, fundamental tensor analysis tools, have been actively developed to solve tensor completion tasks. However, standard tensor decomposition models have not been designed to learn relationships of dimensions along each mode, which limits to accurate tensor completion. Also, previously developed tensor decomposition models have required prior knowledge between relations within dimensions to model the relations, expensive to obtain. This paper proposes TGL (Tensor Decomposition Learning Global and Local Structures) to accurately predict missing entries in tensors. TGL reconstructs a tensor with factor matrices which learn local structures with GNN without prior knowledges. Extensive experiments are conducted to evaluate TGL with baselines and datasets.

Tensor Completion for Surrogate Modeling of Material Property Prediction

When designing materials to optimize certain properties, there are often many possible configurations of designs that need to be explored. For example, the materials' composition of elements will affect properties such as strength or conductivity, which are necessary to know when developing new materials. Exploring all combinations of elements to find optimal materials becomes very time consuming, especially when there are more design variables. For this reason, there is growing interest in using machine learning (ML) to predict a material's properties. In this work, we model the optimization of certain material properties as a tensor completion problem, to leverage the structure of our datasets and navigate the vast number of combinations of material configurations. Across a variety of material property prediction tasks, our experiments show tensor completion methods achieving 10-20% decreased error compared with baseline ML models such as GradientBoosting and Multilayer Perceptron (MLP), while maintaining similar training speed.

Automating Data Science Pipelines with Tensor Completion

Hyperparameter optimization is an essential component in many data science pipelines and typically entails exhaustive time and resource-consuming computations in order to explore the combinatorial search space. Similar to this problem, other key operations in data science pipelines exhibit the exact same properties. Important examples are: neural architecture search, where the goal is to identify the best design choices for a neural network, and query cardinality estimation, where given different predicate values for a SQL query the goal is to estimate the size of the output. In this paper, we abstract away those essential components of data science pipelines and we model them as instances of tensor completion, where each variable of the search space corresponds to one mode of the tensor, and the goal is to identify all missing entries of the tensor, corresponding to all combinations of variable values, starting from a very small sample of observed entries. In order to do so, we first conduct a thorough experimental evaluation of existing state-of-the-art tensor completion techniques and introduce domain-inspired adaptations (such as smoothness across the discretized variable space) and an ensemble technique which is able to achieve state-of-the-art performance. We extensively evaluate existing and proposed methods in a number of datasets generated corresponding to (a) hyperparameter optimization for non-neural network models, (b) neural architecture search, and (c) variants of query cardinality estimation, demonstrating the effectiveness of tensor completion as a tool for automating data science pipelines. Furthermore, we release our generated datasets and code in order to provide benchmarks for future work on this topic.

TRAWL: Tensor Reduced and Approximated Weights for Large Language Models

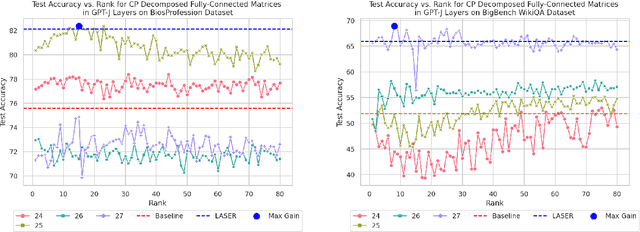
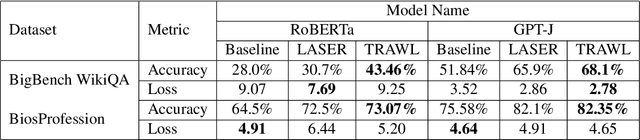
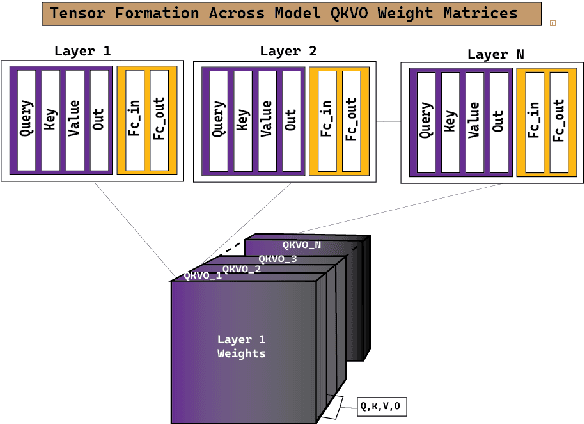
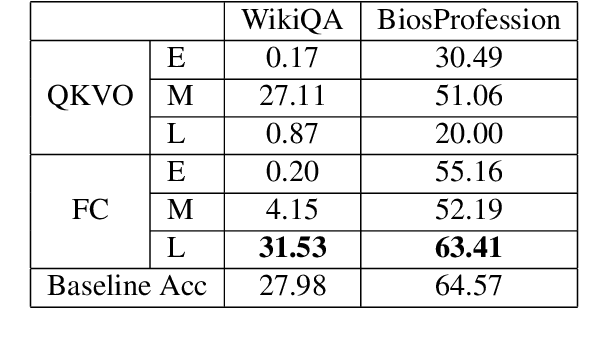
Large language models (LLMs) have fundamentally transformed artificial intelligence, catalyzing recent advancements while imposing substantial environmental and computational burdens. We introduce TRAWL (Tensor Reduced and Approximated Weights for Large Language Models), a novel methodology for optimizing LLMs through tensor decomposition. TRAWL leverages diverse strategies to exploit matrices within transformer-based architectures, realizing notable performance enhancements without necessitating retraining. The most significant improvements were observed through a layer-by-layer intervention strategy, particularly when applied to fully connected weights of the final layers, yielding up to 16% enhancement in accuracy without the need for additional data or fine-tuning. These results underscore the importance of targeted and adaptive techniques in increasing the efficiency and effectiveness of large language model optimization, thereby promoting the development of more sustainable and accessible AI systems.

Time-Aware Tensor Decomposition for Missing Entry Prediction

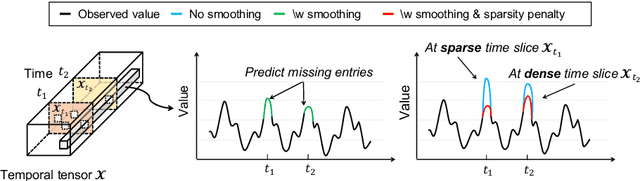
Given a time-evolving tensor with missing entries, how can we effectively factorize it for precisely predicting the missing entries? Tensor factorization has been extensively utilized for analyzing various multi-dimensional real-world data. However, existing models for tensor factorization have disregarded the temporal property for tensor factorization while most real-world data are closely related to time. Moreover, they do not address accuracy degradation due to the sparsity of time slices. The essential problems of how to exploit the temporal property for tensor decomposition and consider the sparsity of time slices remain unresolved. In this paper, we propose TATD (Time-Aware Tensor Decomposition), a novel tensor decomposition method for real-world temporal tensors. TATD is designed to exploit temporal dependency and time-varying sparsity of real-world temporal tensors. We propose a new smoothing regularization with Gaussian kernel for modeling time dependency. Moreover, we improve the performance of TATD by considering time-varying sparsity. We design an alternating optimization scheme suitable for temporal tensor factorization with our smoothing regularization. Extensive experiments show that TATD provides the state-of-the-art accuracy for decomposing temporal tensors.