Fast and Accurate Dual-Way Streaming PARAFAC2 for Irregular Tensors -- Algorithm and Application

How can we efficiently and accurately analyze an irregular tensor in a dual-way streaming setting where the sizes of two dimensions of the tensor increase over time? What types of anomalies are there in the dual-way streaming setting? An irregular tensor is a collection of matrices whose column lengths are the same while their row lengths are different. In a dual-way streaming setting, both new rows of existing matrices and new matrices arrive over time. PARAFAC2 decomposition is a crucial tool for analyzing irregular tensors. Although real-time analysis is necessary in the dual-way streaming, static PARAFAC2 decomposition methods fail to efficiently work in this setting since they perform PARAFAC2 decomposition for accumulated tensors whenever new data arrive. Existing streaming PARAFAC2 decomposition methods work in a limited setting and fail to handle new rows of matrices efficiently. In this paper, we propose Dash, an efficient and accurate PARAFAC2 decomposition method working in the dual-way streaming setting. When new data are given, Dash efficiently performs PARAFAC2 decomposition by carefully dividing the terms related to old and new data and avoiding naive computations involved with old data. Furthermore, applying a forgetting factor makes Dash follow recent movements. Extensive experiments show that Dash achieves up to 14.0x faster speed than existing PARAFAC2 decomposition methods for newly arrived data. We also provide discoveries for detecting anomalies in real-world datasets, including Subprime Mortgage Crisis and COVID-19.

Accurate Open-set Recognition for Memory Workload

How can we accurately identify new memory workloads while classifying known memory workloads? Verifying DRAM (Dynamic Random Access Memory) using various workloads is an important task to guarantee the quality of DRAM. A crucial component in the process is open-set recognition which aims to detect new workloads not seen in the training phase. Despite its importance, however, existing open-set recognition methods are unsatisfactory in terms of accuracy since they fail to exploit the characteristics of workload sequences. In this paper, we propose Acorn, an accurate open-set recognition method capturing the characteristics of workload sequences. Acorn extracts two types of feature vectors to capture sequential patterns and spatial locality patterns in memory access. Acorn then uses the feature vectors to accurately classify a subsequence into one of the known classes or identify it as the unknown class. Experiments show that Acorn achieves state-of-the-art accuracy, giving up to 37% points higher unknown class detection accuracy while achieving comparable known class classification accuracy than existing methods.

DPar2: Fast and Scalable PARAFAC2 Decomposition for Irregular Dense Tensors

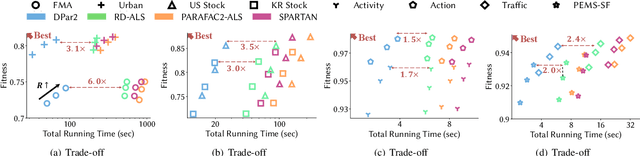
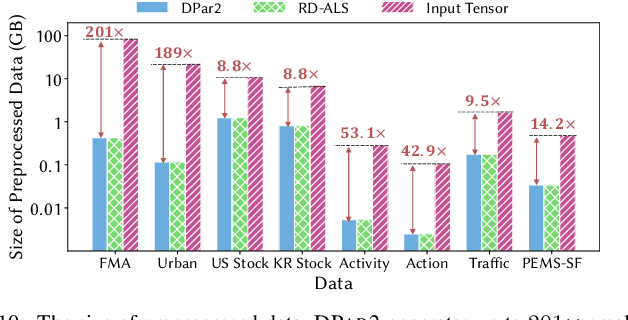
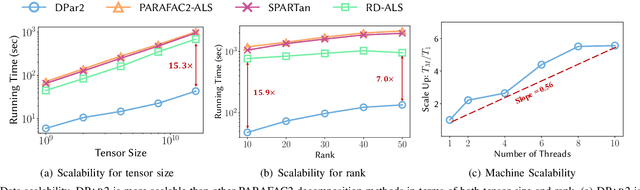
Given an irregular dense tensor, how can we efficiently analyze it? An irregular tensor is a collection of matrices whose columns have the same size and rows have different sizes from each other. PARAFAC2 decomposition is a fundamental tool to deal with an irregular tensor in applications including phenotype discovery and trend analysis. Although several PARAFAC2 decomposition methods exist, their efficiency is limited for irregular dense tensors due to the expensive computations involved with the tensor. In this paper, we propose DPar2, a fast and scalable PARAFAC2 decomposition method for irregular dense tensors. DPar2 achieves high efficiency by effectively compressing each slice matrix of a given irregular tensor, careful reordering of computations with the compression results, and exploiting the irregularity of the tensor. Extensive experiments show that DPar2 is up to 6.0x faster than competitors on real-world irregular tensors while achieving comparable accuracy. In addition, DPar2 is scalable with respect to the tensor size and target rank.

Time-Aware Tensor Decomposition for Missing Entry Prediction

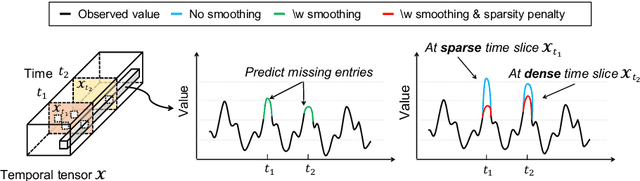
Given a time-evolving tensor with missing entries, how can we effectively factorize it for precisely predicting the missing entries? Tensor factorization has been extensively utilized for analyzing various multi-dimensional real-world data. However, existing models for tensor factorization have disregarded the temporal property for tensor factorization while most real-world data are closely related to time. Moreover, they do not address accuracy degradation due to the sparsity of time slices. The essential problems of how to exploit the temporal property for tensor decomposition and consider the sparsity of time slices remain unresolved. In this paper, we propose TATD (Time-Aware Tensor Decomposition), a novel tensor decomposition method for real-world temporal tensors. TATD is designed to exploit temporal dependency and time-varying sparsity of real-world temporal tensors. We propose a new smoothing regularization with Gaussian kernel for modeling time dependency. Moreover, we improve the performance of TATD by considering time-varying sparsity. We design an alternating optimization scheme suitable for temporal tensor factorization with our smoothing regularization. Extensive experiments show that TATD provides the state-of-the-art accuracy for decomposing temporal tensors.

Fast Partial Fourier Transform

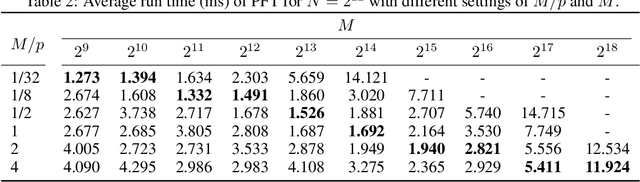
Given a time series vector, how can we efficiently compute a specified part of Fourier coefficients? Fast Fourier transform (FFT) is a widely used algorithm that computes the discrete Fourier transform in many machine learning applications. Despite its pervasive use, all known FFT algorithms do not provide a fine-tuning option for the user to specify one's demand, that is, the output size (the number of Fourier coefficients to be computed) is algorithmically determined by the input size. This matters because not every application using FFT requires the whole spectrum of the frequency domain, resulting in an inefficiency due to extra computation. In this paper, we propose a fast Partial Fourier Transform (PFT), a careful modification of the Cooley-Tukey algorithm that enables one to specify an arbitrary consecutive range where the coefficients should be computed. We derive the asymptotic time complexity of PFT with respect to input and output sizes, as well as its numerical accuracy. Experimental results show that our algorithm outperforms the state-of-the-art FFT algorithms, with an order of magnitude of speedup for sufficiently small output sizes without sacrificing accuracy.

FALCON: Fast and Lightweight Convolution for Compressing and Accelerating CNN

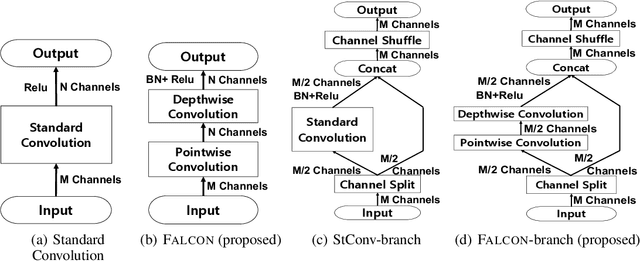
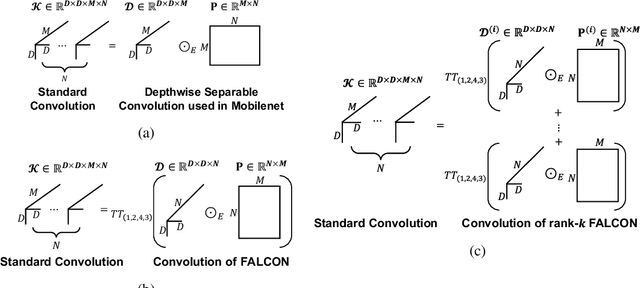
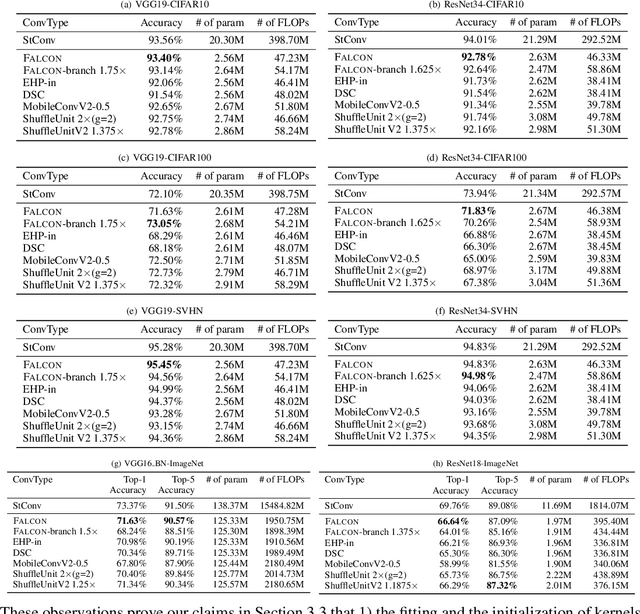
How can we efficiently compress Convolutional Neural Networks (CNN) while retaining their accuracy on classification tasks? A promising direction is based on depthwise separable convolution which replaces a standard convolution with a depthwise convolution and a pointwise convolution. However, previous works based on depthwise separable convolution are limited since 1) they are mostly heuristic approaches without a precise understanding of their relations to standard convolution, and 2) their accuracies do not match that of the standard convolution. In this paper, we propose FALCON, an accurate and lightweight method for compressing CNN. FALCON is derived by interpreting existing convolution methods based on depthwise separable convolution using EHP, our proposed mathematical formulation to approximate the standard convolution kernel. Such interpretation leads to developing a generalized version rank-k FALCON which further improves the accuracy while sacrificing a bit of compression and computation reduction rates. In addition, we propose FALCON-branch by fitting FALCON into the previous state-of-the-art convolution unit ShuffleUnitV2 which gives even better accuracy. Experiments show that FALCON and FALCON-branch outperform 1) existing methods based on depthwise separable convolution and 2) standard CNN models by up to 8x compression and 8x computation reduction while ensuring similar accuracy. We also demonstrate that rank-k FALCON provides even better accuracy than standard convolution in many cases, while using a smaller number of parameters and floating-point operations.