DPar2: Fast and Scalable PARAFAC2 Decomposition for Irregular Dense Tensors
Paper and Code
Mar 24, 2022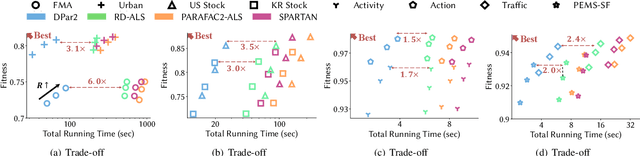
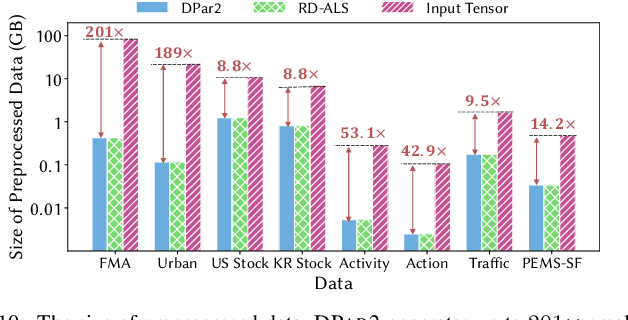
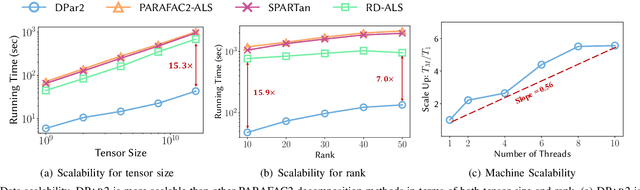

Given an irregular dense tensor, how can we efficiently analyze it? An irregular tensor is a collection of matrices whose columns have the same size and rows have different sizes from each other. PARAFAC2 decomposition is a fundamental tool to deal with an irregular tensor in applications including phenotype discovery and trend analysis. Although several PARAFAC2 decomposition methods exist, their efficiency is limited for irregular dense tensors due to the expensive computations involved with the tensor. In this paper, we propose DPar2, a fast and scalable PARAFAC2 decomposition method for irregular dense tensors. DPar2 achieves high efficiency by effectively compressing each slice matrix of a given irregular tensor, careful reordering of computations with the compression results, and exploiting the irregularity of the tensor. Extensive experiments show that DPar2 is up to 6.0x faster than competitors on real-world irregular tensors while achieving comparable accuracy. In addition, DPar2 is scalable with respect to the tensor size and target rank.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge