Fast Partial Fourier Transform
Paper and Code
Aug 28, 2020


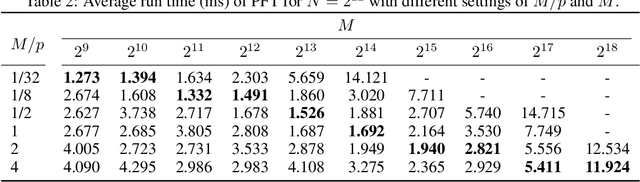
Given a time series vector, how can we efficiently compute a specified part of Fourier coefficients? Fast Fourier transform (FFT) is a widely used algorithm that computes the discrete Fourier transform in many machine learning applications. Despite its pervasive use, all known FFT algorithms do not provide a fine-tuning option for the user to specify one's demand, that is, the output size (the number of Fourier coefficients to be computed) is algorithmically determined by the input size. This matters because not every application using FFT requires the whole spectrum of the frequency domain, resulting in an inefficiency due to extra computation. In this paper, we propose a fast Partial Fourier Transform (PFT), a careful modification of the Cooley-Tukey algorithm that enables one to specify an arbitrary consecutive range where the coefficients should be computed. We derive the asymptotic time complexity of PFT with respect to input and output sizes, as well as its numerical accuracy. Experimental results show that our algorithm outperforms the state-of-the-art FFT algorithms, with an order of magnitude of speedup for sufficiently small output sizes without sacrificing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge