Tensor Convolutional Network for Higher-Order Interaction Prediction in Sparse Tensors

Many real-world data, such as recommendation data and temporal graphs, can be represented as incomplete sparse tensors where most entries are unobserved. For such sparse tensors, identifying the top-k higher-order interactions that are most likely to occur among unobserved ones is crucial. Tensor factorization (TF) has gained significant attention in various tensor-based applications, serving as an effective method for finding these top-k potential interactions. However, existing TF methods primarily focus on effectively fusing latent vectors of entities, which limits their expressiveness. Since most entities in sparse tensors have only a few interactions, their latent representations are often insufficiently trained. In this paper, we propose TCN, an accurate and compatible tensor convolutional network that integrates seamlessly with existing TF methods for predicting higher-order interactions. We design a highly effective encoder to generate expressive latent vectors of entities. To achieve this, we propose to (1) construct a graph structure derived from a sparse tensor and (2) develop a relation-aware encoder, TCN, that learns latent representations of entities by leveraging the graph structure. Since TCN complements traditional TF methods, we seamlessly integrate TCN with existing TF methods, enhancing the performance of predicting top-k interactions. Extensive experiments show that TCN integrated with a TF method outperforms competitors, including TF methods and a hyperedge prediction method. Moreover, TCN is broadly compatible with various TF methods and GNNs (Graph Neural Networks), making it a versatile solution.

Retrieval Based Time Series Forecasting

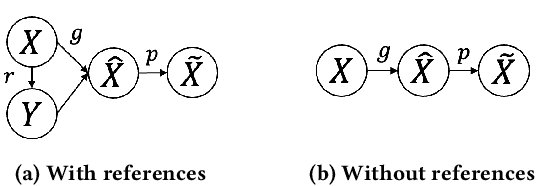
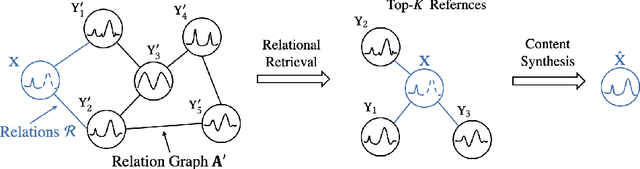
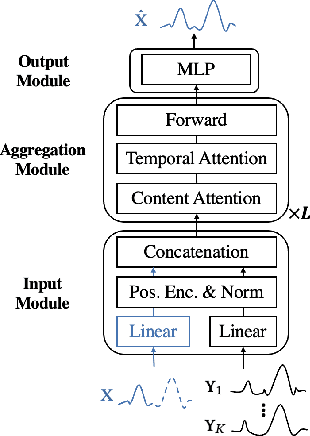
Time series data appears in a variety of applications such as smart transportation and environmental monitoring. One of the fundamental problems for time series analysis is time series forecasting. Despite the success of recent deep time series forecasting methods, they require sufficient observation of historical values to make accurate forecasting. In other words, the ratio of the output length (or forecasting horizon) to the sum of the input and output lengths should be low enough (e.g., 0.3). As the ratio increases (e.g., to 0.8), the uncertainty for the forecasting accuracy increases significantly. In this paper, we show both theoretically and empirically that the uncertainty could be effectively reduced by retrieving relevant time series as references. In the theoretical analysis, we first quantify the uncertainty and show its connections to the Mean Squared Error (MSE). Then we prove that models with references are easier to learn than models without references since the retrieved references could reduce the uncertainty. To empirically demonstrate the effectiveness of the retrieval based time series forecasting models, we introduce a simple yet effective two-stage method, called ReTime consisting of a relational retrieval and a content synthesis. We also show that ReTime can be easily adapted to the spatial-temporal time series and time series imputation settings. Finally, we evaluate ReTime on real-world datasets to demonstrate its effectiveness.

Deep Active Learning by Leveraging Training Dynamics

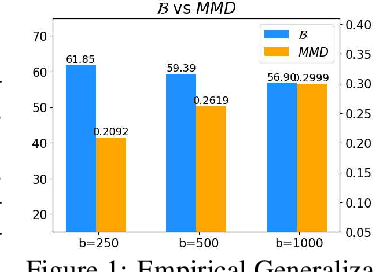
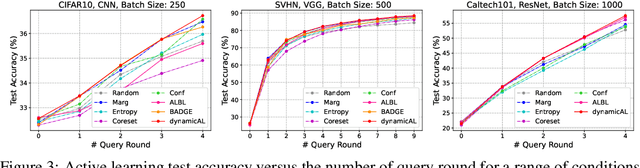
Active learning theories and methods have been extensively studied in classical statistical learning settings. However, deep active learning, i.e., active learning with deep learning models, is usually based on empirical criteria without solid theoretical justification, thus suffering from heavy doubts when some of those fail to provide benefits in applications. In this paper, by exploring the connection between the generalization performance and the training dynamics, we propose a theory-driven deep active learning method (dynamicAL) which selects samples to maximize training dynamics. In particular, we prove that convergence speed of training and the generalization performance is positively correlated under the ultra-wide condition and show that maximizing the training dynamics leads to a better generalization performance. Further on, to scale up to large deep neural networks and data sets, we introduce two relaxations for the subset selection problem and reduce the time complexity from polynomial to constant. Empirical results show that dynamicAL not only outperforms the other baselines consistently but also scales well on large deep learning models. We hope our work inspires more attempts in bridging the theoretical findings of deep networks and practical impacts in deep active learning applications.