On the Role of Preprocessing and Memristor Dynamics in Reservoir Computing for Image Classification

Reservoir computing (RC) is an emerging recurrent neural network architecture that has attracted growing attention for its low training cost and modest hardware requirements. Memristor-based circuits are particularly promising for RC, as their intrinsic dynamics can reduce network size and parameter overhead in tasks such as time-series prediction and image recognition. Although RC has been demonstrated with several memristive devices, a comprehensive evaluation of device-level requirements remains limited. In this paper, we analyze and explain the operation of a parallel delayed feedback network (PDFN) RC architecture with volatile memristors, focusing on how device characteristics -- such as decay rate, quantization, and variability -- affect reservoir performance. We further discuss strategies to improve data representation in the reservoir using preprocessing methods and suggest potential improvements. The proposed approach achieves 95.89% classification accuracy on MNIST, comparable with the best reported memristor-based RC implementations. Furthermore, the method maintains high robustness under 20% device variability, achieving an accuracy of up to 94.2%. These results demonstrate that volatile memristors can support reliable spatio-temporal information processing and reinforce their potential as key building blocks for compact, high-speed, and energy-efficient neuromorphic computing systems.

Preprocessing Methods for Memristive Reservoir Computing for Image Recognition

Reservoir computing (RC) has attracted attention as an efficient recurrent neural network architecture due to its simplified training, requiring only its last perceptron readout layer to be trained. When implemented with memristors, RC systems benefit from their dynamic properties, which make them ideal for reservoir construction. However, achieving high performance in memristor-based RC remains challenging, as it critically depends on the input preprocessing method and reservoir size. Despite growing interest, a comprehensive evaluation that quantifies the impact of these factors is still lacking. This paper systematically compares various preprocessing methods for memristive RC systems, assessing their effects on accuracy and energy consumption. We also propose a parity-based preprocessing method that improves accuracy by 2-6% while requiring only a modest increase in device count compared to other methods. Our findings highlight the importance of informed preprocessing strategies to improve the efficiency and scalability of memristive RC systems.

Viral Load Inference in Non-Adaptive Pooled Testing

Medical diagnostic testing can be made significantly more efficient using pooled testing protocols. These typically require a sparse infection signal and use either binary or real-valued entries of O(1). However, existing methods do not allow for inferring viral loads which span many orders of magnitude. We develop a message passing algorithm coupled with a PCR (Polymerase Chain Reaction) specific noise function to allow accurate inference of realistic viral load signals. This work is in the non-adaptive setting and could open the possibility of efficient screening where viral load determination is clinically important.

Scalable Node-Disjoint and Edge-Disjoint Multi-wavelength Routing

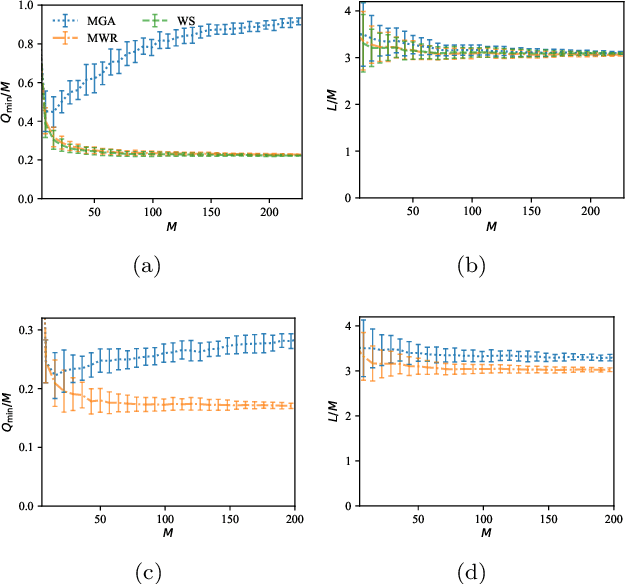
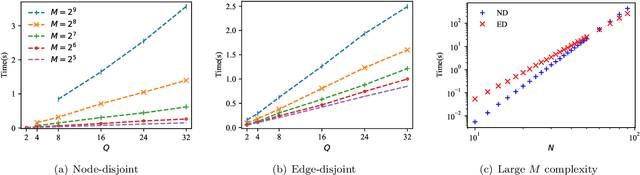
Probabilistic message-passing algorithms are developed for routing transmissions in multi-wavelength optical communication networks, under node and edge-disjoint routing constraints and for various objective functions. Global routing optimization is a hard computational task on its own but is made much more difficult under the node/edge-disjoint constraints and in the presence of multiple wavelengths, a problem which dominates routing efficiency in real optical communication networks that carry most of the world's Internet traffic. The scalable principled method we have developed is exact on trees but provides good approximate solutions on locally tree-like graphs. It accommodates a variety of objective functions that correspond to low latency, load balancing and consolidation of routes, and can be easily extended to include heterogeneous signal-to-noise values on edges and a restriction on the available wavelengths per edge. It can be used for routing and managing transmissions on existing topologies as well as for designing and modifying optical communication networks. Additionally, it provides the tool for settling an open and much debated question on the merit of wavelength-switching nodes and the added capabilities they provide. The methods have been tested on generated networks such as random-regular, Erd\H{o}s R\'{e}nyi and power-law graphs, as well as on the UK and US optical communication networks. They show excellent performance with respect to existing methodology on small networks and have been scaled up to network sizes that are beyond the reach of most existing algorithms.

The Space of Functions Computed by Deep Layered Machines

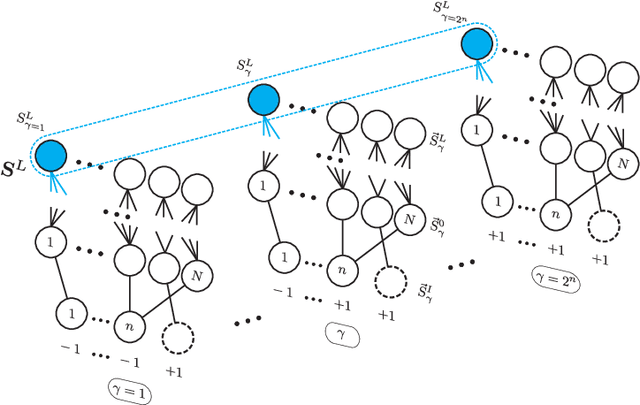
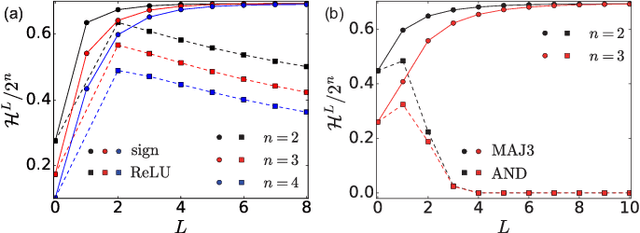
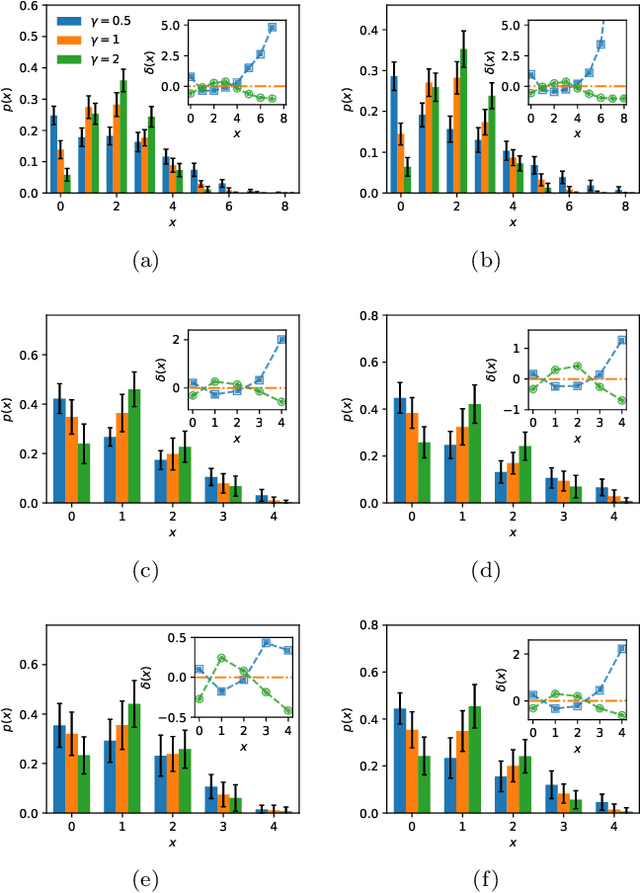
We study the space of functions computed by random layered machines, including deep neural networks, and Boolean circuits. Investigating the distribution of Boolean functions computed on the recurrent and layer-dependent architectures, we find that it is the same in both models. Depending on the initial conditions and computing elements used, we characterize the space of functions computed at the large depth limit and show that the macroscopic entropy of Boolean functions is either monotonically increasing or decreasing with the growing depth.

Scalable Influence Estimation Without Sampling

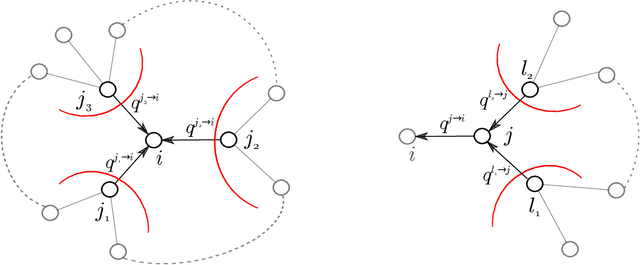
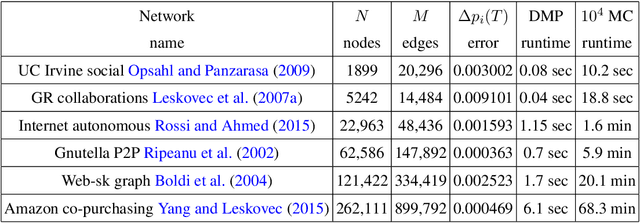
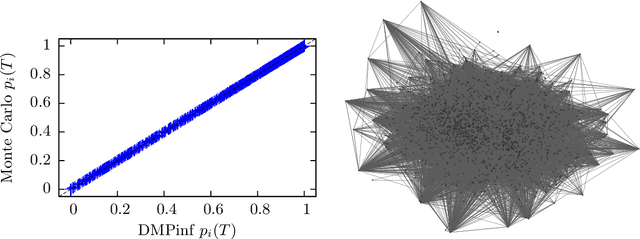
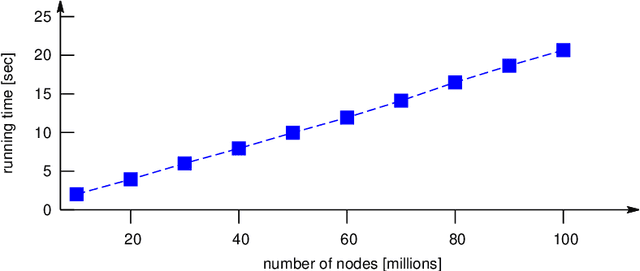
In a diffusion process on a network, how many nodes are expected to be influenced by a set of initial spreaders? This natural problem, often referred to as influence estimation, boils down to computing the marginal probability that a given node is active at a given time when the process starts from specified initial condition. Among many other applications, this task is crucial for a well-studied problem of influence maximization: finding optimal spreaders in a social network that maximize the influence spread by a certain time horizon. Indeed, influence estimation needs to be called multiple times for comparing candidate seed sets. Unfortunately, in many models of interest an exact computation of marginals is #P-hard. In practice, influence is often estimated using Monte-Carlo sampling methods that require a large number of runs for obtaining a high-fidelity prediction, especially at large times. It is thus desirable to develop analytic techniques as an alternative to sampling methods. Here, we suggest an algorithm for estimating the influence function in popular independent cascade model based on a scalable dynamic message-passing approach. This method has a computational complexity of a single Monte-Carlo simulation and provides an upper bound on the expected spread on a general graph, yielding exact answer for treelike networks. We also provide dynamic message-passing equations for a stochastic version of the linear threshold model. The resulting saving of a potentially large sampling factor in the running time compared to simulation-based techniques hence makes it possible to address large-scale problem instances.

Large Deviation Analysis of Function Sensitivity in Random Deep Neural Networks

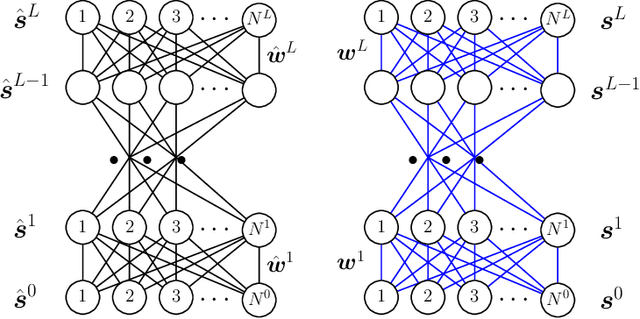
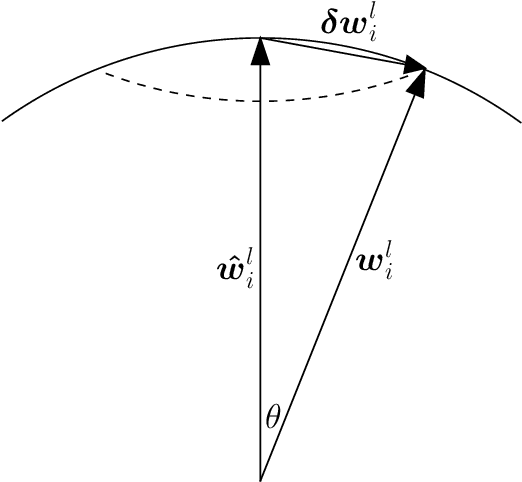
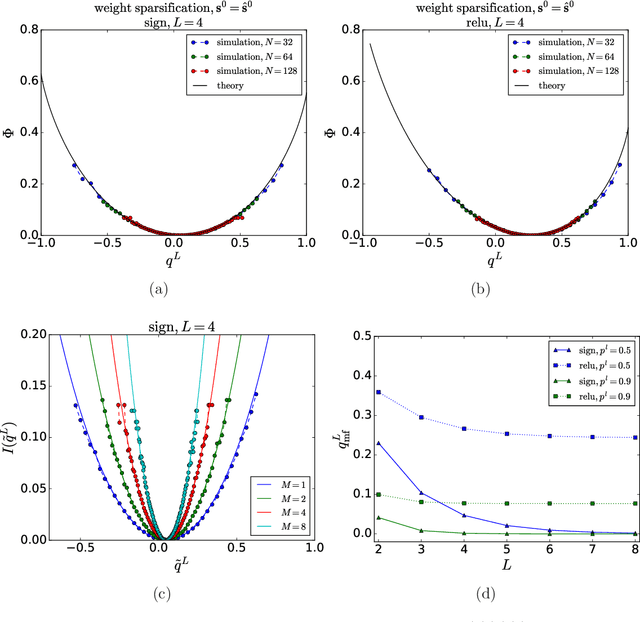
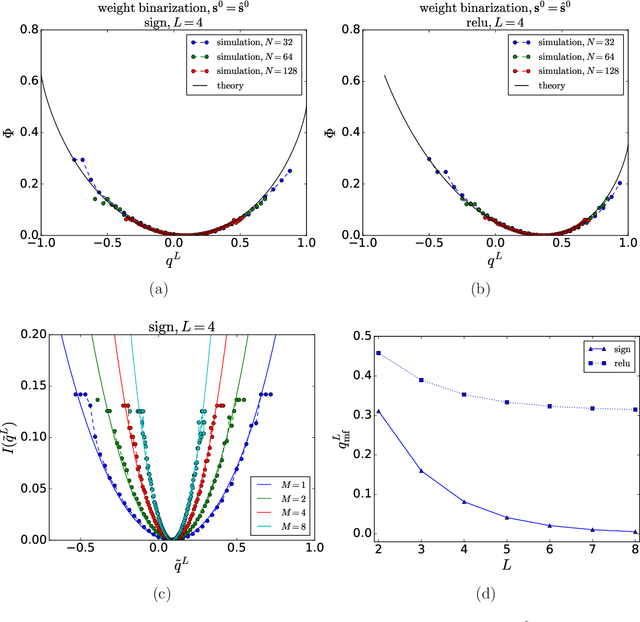
Mean field theory has been successfully used to analyze deep neural networks (DNN) in the infinite size limit. Given the finite size of realistic DNN, we utilize the large deviation theory and path integral analysis to study the deviation of functions represented by DNN from their typical mean field solutions. The parameter perturbations investigated include weight sparsification (dilution) and binarization, which are commonly used in model simplification, for both ReLU and sign activation functions. We find that random networks with ReLU activation are more robust to parameter perturbations with respect to their counterparts with sign activation, which arguably is reflected in the simplicity of the functions they generate.

Exploring the Function Space of Deep-Learning Machines

The function space of deep-learning machines is investigated by studying growth in the entropy of functions of a given error with respect to a reference function, realized by a deep-learning machine. Using physics-inspired methods we study both sparsely and densely-connected architectures to discover a layer-wise convergence of candidate functions, marked by a corresponding reduction in entropy when approaching the reference function, gain insight into the importance of having a large number of layers, and observe phase transitions as the error increases.