Scalable Node-Disjoint and Edge-Disjoint Multi-wavelength Routing

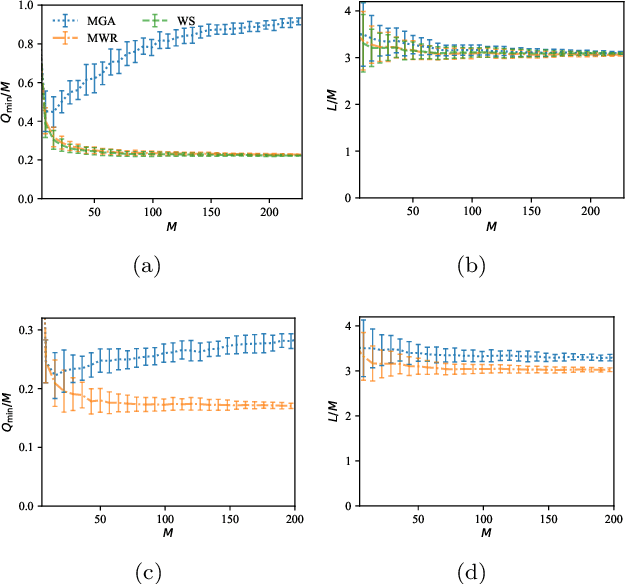
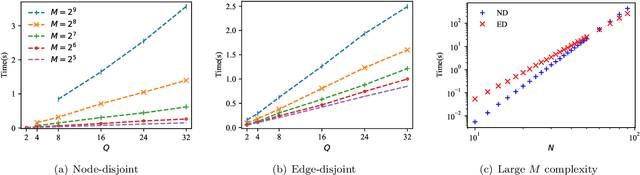
Probabilistic message-passing algorithms are developed for routing transmissions in multi-wavelength optical communication networks, under node and edge-disjoint routing constraints and for various objective functions. Global routing optimization is a hard computational task on its own but is made much more difficult under the node/edge-disjoint constraints and in the presence of multiple wavelengths, a problem which dominates routing efficiency in real optical communication networks that carry most of the world's Internet traffic. The scalable principled method we have developed is exact on trees but provides good approximate solutions on locally tree-like graphs. It accommodates a variety of objective functions that correspond to low latency, load balancing and consolidation of routes, and can be easily extended to include heterogeneous signal-to-noise values on edges and a restriction on the available wavelengths per edge. It can be used for routing and managing transmissions on existing topologies as well as for designing and modifying optical communication networks. Additionally, it provides the tool for settling an open and much debated question on the merit of wavelength-switching nodes and the added capabilities they provide. The methods have been tested on generated networks such as random-regular, Erd\H{o}s R\'{e}nyi and power-law graphs, as well as on the UK and US optical communication networks. They show excellent performance with respect to existing methodology on small networks and have been scaled up to network sizes that are beyond the reach of most existing algorithms.

Generalized minimum dominating set and application in automatic text summarization

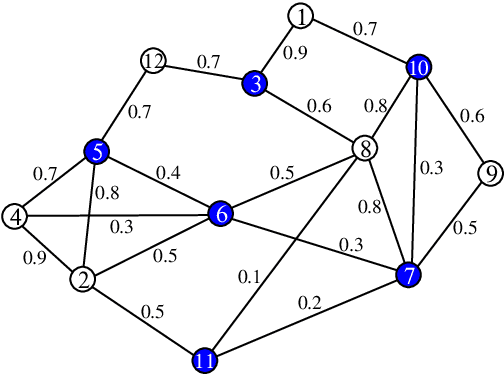
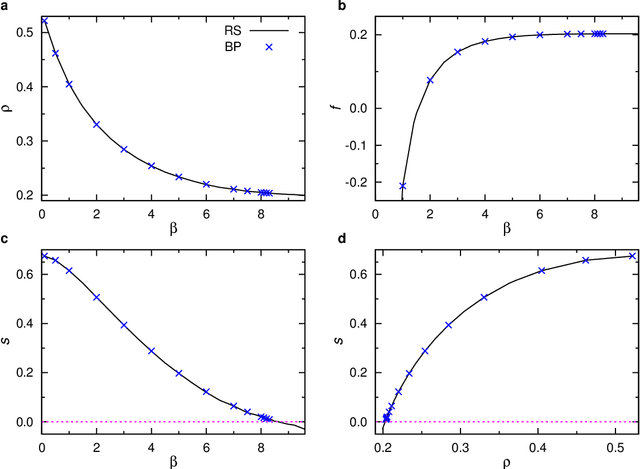
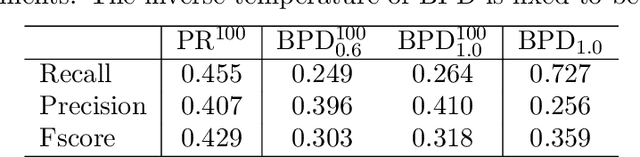
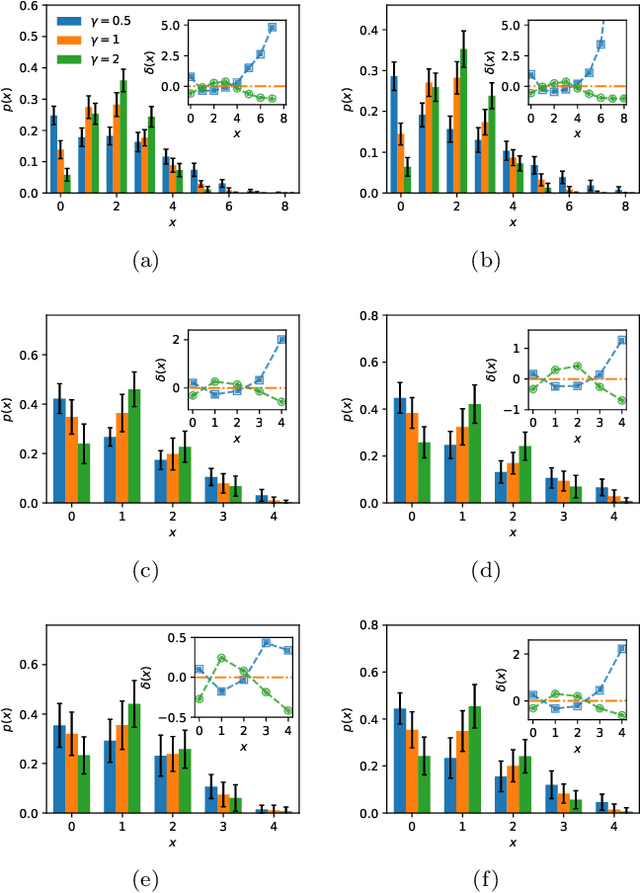
For a graph formed by vertices and weighted edges, a generalized minimum dominating set (MDS) is a vertex set of smallest cardinality such that the summed weight of edges from each outside vertex to vertices in this set is equal to or larger than certain threshold value. This generalized MDS problem reduces to the conventional MDS problem in the limiting case of all the edge weights being equal to the threshold value. We treat the generalized MDS problem in the present paper by a replica-symmetric spin glass theory and derive a set of belief-propagation equations. As a practical application we consider the problem of extracting a set of sentences that best summarize a given input text document. We carry out a preliminary test of the statistical physics-inspired method to this automatic text summarization problem.