Exploring Loss Landscapes through the Lens of Spin Glass Theory

In the past decade, significant strides in deep learning have led to numerous groundbreaking applications. Despite these advancements, the understanding of the high generalizability of deep learning, especially in such an over-parametrized space, remains limited. Successful applications are often considered as empirical rather than scientific achievements. For instance, deep neural networks' (DNNs) internal representations, decision-making mechanism, absence of overfitting in an over-parametrized space, high generalizability, etc., remain less understood. This paper delves into the loss landscape of DNNs through the lens of spin glass in statistical physics, i.e. a system characterized by a complex energy landscape with numerous metastable states, to better understand how DNNs work. We investigated a single hidden layer Rectified Linear Unit (ReLU) neural network model, and introduced several protocols to examine the analogy between DNNs (trained with datasets including MNIST and CIFAR10) and spin glass. Specifically, we used (1) random walk in the parameter space of DNNs to unravel the structures in their loss landscape; (2) a permutation-interpolation protocol to study the connection between copies of identical regions in the loss landscape due to the permutation symmetry in the hidden layers; (3) hierarchical clustering to reveal the hierarchy among trained solutions of DNNs, reminiscent of the so-called Replica Symmetry Breaking (RSB) phenomenon (i.e. the Parisi solution) in analogy to spin glass; (4) finally, we examine the relationship between the degree of the ruggedness of the loss landscape of the DNN and its generalizability, showing an improvement of flattened minima.

Understanding the stochastic dynamics of sequential decision-making processes: A path-integral analysis of Multi-armed Bandits

The multi-armed bandit (MAB) model is one of the most classical models to study decision-making in an uncertain environment. In this model, a player needs to choose one of K possible arms of a bandit machine to play at each time step, where the corresponding arm returns a random reward to the player, potentially from a specific unknown distribution. The target of the player is to collect as much rewards as possible during the process. Despite its simplicity, the MAB model offers an excellent playground for studying the trade-off between exploration versus exploitation and designing effective algorithms for sequential decision-making under uncertainty. Although many asymptotically optimal algorithms have been established, the finite-time behaviours of the stochastic dynamics of the MAB model appears much more difficult to analyze, due to the intertwining between the decision-making and the rewards being collected. In this paper, we employ techniques in statistical physics to analyze the MAB model, which facilitates to characterize the distribution of cumulative regrets at a finite short time, the central quantity of interest in an MAB algorithm, as well as the intricate dynamical behaviours of the model.

Scalable Node-Disjoint and Edge-Disjoint Multi-wavelength Routing

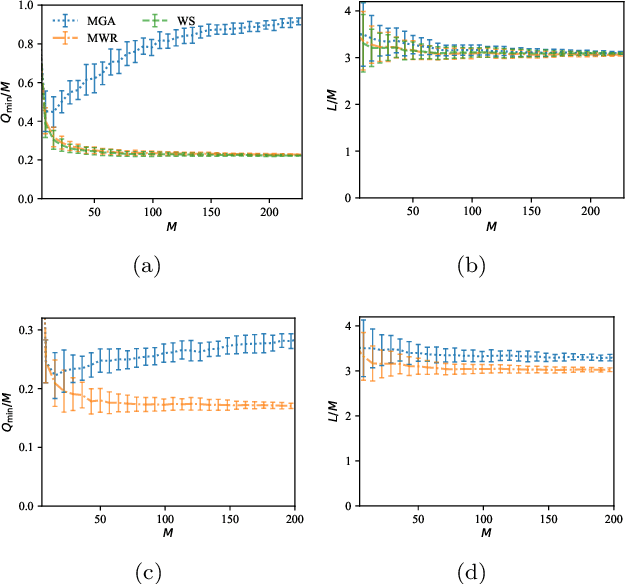
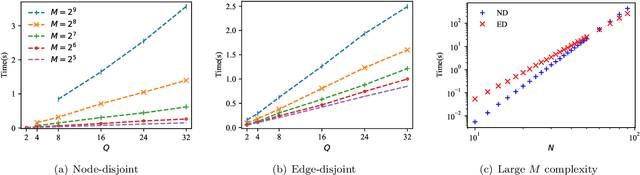
Probabilistic message-passing algorithms are developed for routing transmissions in multi-wavelength optical communication networks, under node and edge-disjoint routing constraints and for various objective functions. Global routing optimization is a hard computational task on its own but is made much more difficult under the node/edge-disjoint constraints and in the presence of multiple wavelengths, a problem which dominates routing efficiency in real optical communication networks that carry most of the world's Internet traffic. The scalable principled method we have developed is exact on trees but provides good approximate solutions on locally tree-like graphs. It accommodates a variety of objective functions that correspond to low latency, load balancing and consolidation of routes, and can be easily extended to include heterogeneous signal-to-noise values on edges and a restriction on the available wavelengths per edge. It can be used for routing and managing transmissions on existing topologies as well as for designing and modifying optical communication networks. Additionally, it provides the tool for settling an open and much debated question on the merit of wavelength-switching nodes and the added capabilities they provide. The methods have been tested on generated networks such as random-regular, Erd\H{o}s R\'{e}nyi and power-law graphs, as well as on the UK and US optical communication networks. They show excellent performance with respect to existing methodology on small networks and have been scaled up to network sizes that are beyond the reach of most existing algorithms.