Backdoor to the Hidden Ground State: Planted Vertex Cover Example

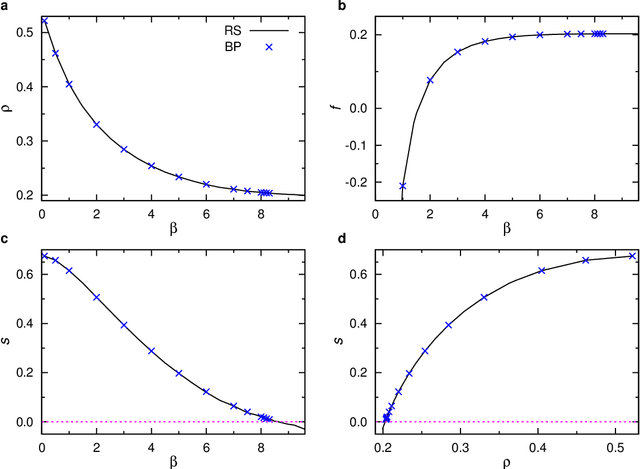
We introduce a planted vertex cover problem on regular random graphs and study it by the cavity method. The equilibrium ordering phase transition of this binary-spin two-body interaction system is discontinuous in nature distinct from the continuous one of conventional Ising-like models, and it is dynamically blocked by an extensive free energy barrier. We discover that the disordered symmetric phase of this system may be locally stable with respect to the ordered phase at all inverse temperatures except for a unique eureka point $\beta_b$ at which it is only marginally stable. The eureka point $\beta_b$ serves as a backdoor to access the hidden ground state with vanishing free energy barrier. It exists in an infinite series of planted random graph ensembles and we determine their structural parameters analytically. The revealed new type of free energy landscape may also exist in other planted random-graph optimization problems at the interface of statistical physics and statistical inference.

Neural-network based general method for statistical mechanics on sparse systems

We propose a general method for solving statistical mechanics problems defined on sparse graphs, such as random graphs, real-world networks, and low-dimensional lattices. Our approach extract a small feedback vertex set of the sparse graph, converting the sparse system to a strongly correlated system with many-body and dense interactions on the feedback set, then solve it using variational method based on neural networks to estimate free energy, observables, and generate unbiased samples via direct sampling. Extensive experiments show that our approach is more accurate than existing approaches for sparse spin glass systems. On random graphs and real-world networks, our approach significantly outperforms the standard methods for sparse systems such as belief-propagation; on structured sparse systems such as two-dimensional lattices our approach is significantly faster and more accurate than recently proposed variational autoregressive networks using convolution neural networks.

Active online learning in the binary perceptron problem

The binary perceptron is the simplest artificial neural network formed by $N$ input units and one output unit, with the neural states and the synaptic weights all restricted to $\pm 1$ values. The task in the teacher--student scenario is to infer the hidden weight vector by training on a set of labeled patterns. Previous efforts on the passive learning mode have shown that learning from independent random patterns is quite inefficient. Here we consider the active online learning mode in which the student designs every new Ising training pattern. We demonstrate that it is mathematically possible to achieve perfect (error-free) inference using only $N$ designed training patterns, but this is computationally unfeasible for large systems. We then investigate two Bayesian statistical designing protocols, which require $2.3 N$ and $1.9 N$ training patterns, respectively, to achieve error-free inference. If the training patterns are instead designed through deductive reasoning, perfect inference is achieved using $N\!+\!\log_{2}\!N$ samples. The performance gap between Bayesian and deductive designing strategies may be shortened in future work by taking into account the possibility of ergodicity breaking in the version space of the binary perceptron.

Unsupervised prototype learning in an associative-memory network

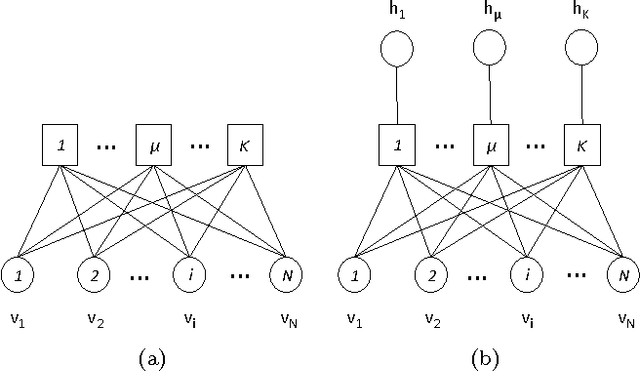
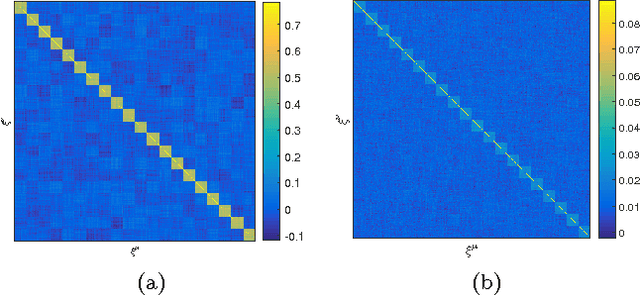
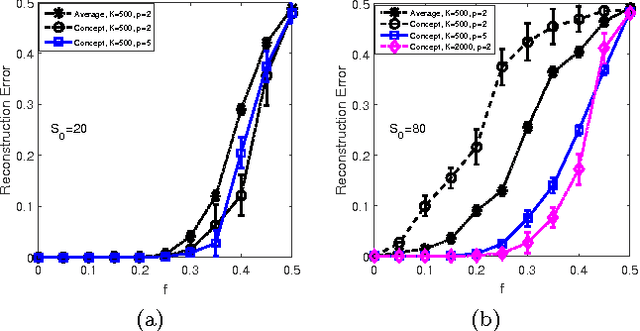
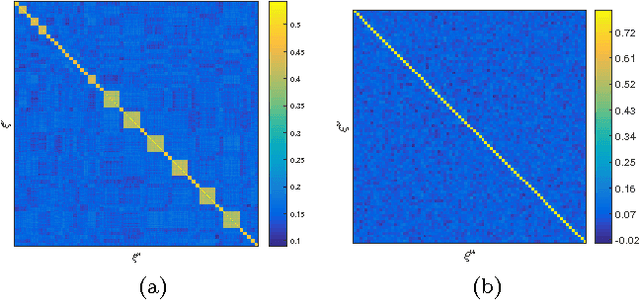
Unsupervised learning in a generalized Hopfield associative-memory network is investigated in this work. First, we prove that the (generalized) Hopfield model is equivalent to a semi-restricted Boltzmann machine with a layer of visible neurons and another layer of hidden binary neurons, so it could serve as the building block for a multilayered deep-learning system. We then demonstrate that the Hopfield network can learn to form a faithful internal representation of the observed samples, with the learned memory patterns being prototypes of the input data. Furthermore, we propose a spectral method to extract a small set of concepts (idealized prototypes) as the most concise summary or abstraction of the empirical data.

Loop-corrected belief propagation for lattice spin models

Belief propagation (BP) is a message-passing method for solving probabilistic graphical models. It is very successful in treating disordered models (such as spin glasses) on random graphs. On the other hand, finite-dimensional lattice models have an abundant number of short loops, and the BP method is still far from being satisfactory in treating the complicated loop-induced correlations in these systems. Here we propose a loop-corrected BP method to take into account the effect of short loops in lattice spin models. We demonstrate, through an application to the square-lattice Ising model, that loop-corrected BP improves over the naive BP method significantly. We also implement loop-corrected BP at the coarse-grained region graph level to further boost its performance.

Generalized minimum dominating set and application in automatic text summarization

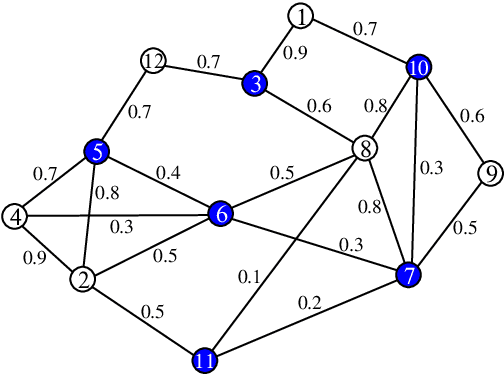
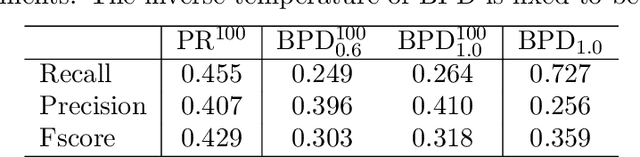
For a graph formed by vertices and weighted edges, a generalized minimum dominating set (MDS) is a vertex set of smallest cardinality such that the summed weight of edges from each outside vertex to vertices in this set is equal to or larger than certain threshold value. This generalized MDS problem reduces to the conventional MDS problem in the limiting case of all the edge weights being equal to the threshold value. We treat the generalized MDS problem in the present paper by a replica-symmetric spin glass theory and derive a set of belief-propagation equations. As a practical application we consider the problem of extracting a set of sentences that best summarize a given input text document. We carry out a preliminary test of the statistical physics-inspired method to this automatic text summarization problem.

Solving the undirected feedback vertex set problem by local search

An undirected graph consists of a set of vertices and a set of undirected edges between vertices. Such a graph may contain an abundant number of cycles, then a feedback vertex set (FVS) is a set of vertices intersecting with each of these cycles. Constructing a FVS of cardinality approaching the global minimum value is a optimization problem in the nondeterministic polynomial-complete complexity class, therefore it might be extremely difficult for some large graph instances. In this paper we develop a simulated annealing local search algorithm for the undirected FVS problem. By defining an order for the vertices outside the FVS, we replace the global cycle constraints by a set of local vertex constraints on this order. Under these local constraints the cardinality of the focal FVS is then gradually reduced by the simulated annealing dynamical process. We test this heuristic algorithm on large instances of Er\"odos-Renyi random graph and regular random graph, and find that this algorithm is comparable in performance to the belief propagation-guided decimation algorithm.