Wei-Mou Zheng
Predicting protein inter-residue contacts using composite likelihood maximization and deep learning
Aug 31, 2018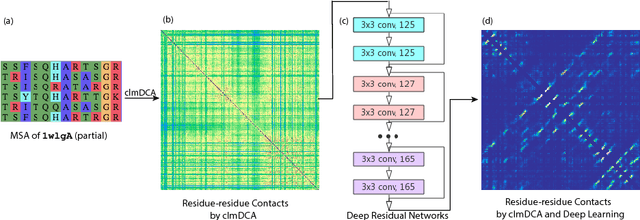
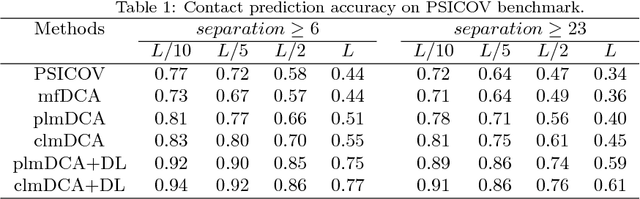
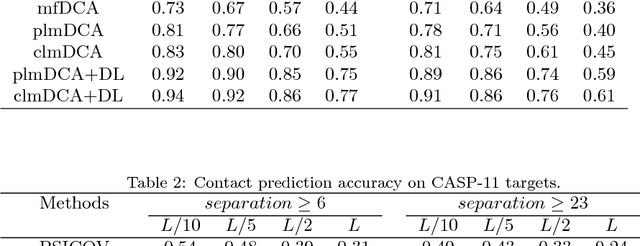
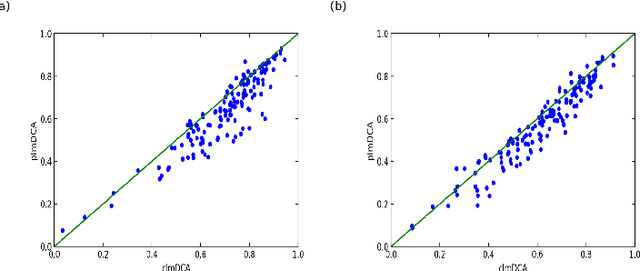
Abstract:Accurate prediction of inter-residue contacts of a protein is important to calcu- lating its tertiary structure. Analysis of co-evolutionary events among residues has been proved effective to inferring inter-residue contacts. The Markov ran- dom field (MRF) technique, although being widely used for contact prediction, suffers from the following dilemma: the actual likelihood function of MRF is accurate but time-consuming to calculate, in contrast, approximations to the actual likelihood, say pseudo-likelihood, are efficient to calculate but inaccu- rate. Thus, how to achieve both accuracy and efficiency simultaneously remains a challenge. In this study, we present such an approach (called clmDCA) for contact prediction. Unlike plmDCA using pseudo-likelihood, i.e., the product of conditional probability of individual residues, our approach uses composite- likelihood, i.e., the product of conditional probability of all residue pairs. Com- posite likelihood has been theoretically proved as a better approximation to the actual likelihood function than pseudo-likelihood. Meanwhile, composite likelihood is still efficient to maximize, thus ensuring the efficiency of clmDCA. We present comprehensive experiments on popular benchmark datasets, includ- ing PSICOV dataset and CASP-11 dataset, to show that: i) clmDCA alone outperforms the existing MRF-based approaches in prediction accuracy. ii) When equipped with deep learning technique for refinement, the prediction ac- curacy of clmDCA was further significantly improved, suggesting the suitability of clmDCA for subsequent refinement procedure. We further present successful application of the predicted contacts to accurately build tertiary structures for proteins in the PSICOV dataset. Accessibility: The software clmDCA and a server are publicly accessible through http://protein.ict.ac.cn/clmDCA/.
Loop-corrected belief propagation for lattice spin models
Feb 16, 2016



Abstract:Belief propagation (BP) is a message-passing method for solving probabilistic graphical models. It is very successful in treating disordered models (such as spin glasses) on random graphs. On the other hand, finite-dimensional lattice models have an abundant number of short loops, and the BP method is still far from being satisfactory in treating the complicated loop-induced correlations in these systems. Here we propose a loop-corrected BP method to take into account the effect of short loops in lattice spin models. We demonstrate, through an application to the square-lattice Ising model, that loop-corrected BP improves over the naive BP method significantly. We also implement loop-corrected BP at the coarse-grained region graph level to further boost its performance.
* 11 pages, minor changes with new references added. Final version as published in EPJB
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge