Scalable Influence Estimation Without Sampling
Paper and Code
Dec 29, 2019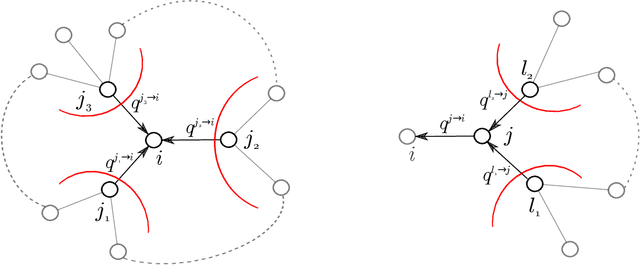
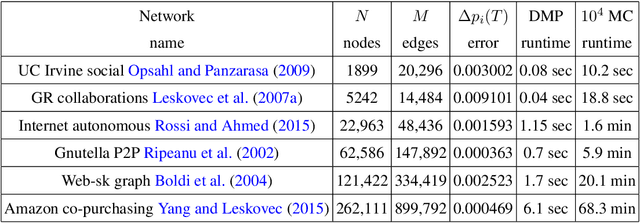
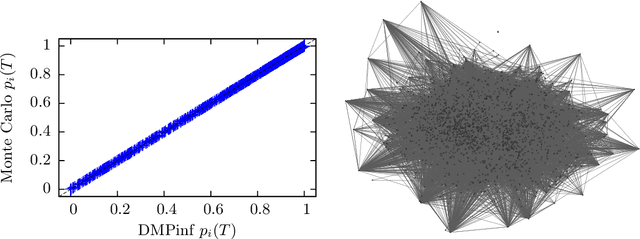
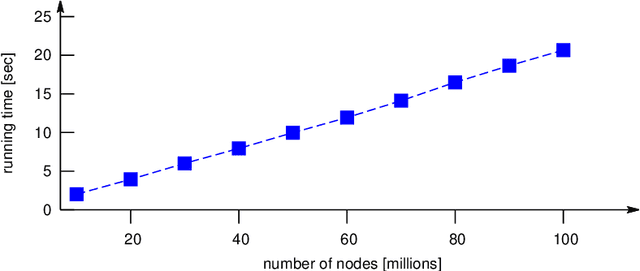
In a diffusion process on a network, how many nodes are expected to be influenced by a set of initial spreaders? This natural problem, often referred to as influence estimation, boils down to computing the marginal probability that a given node is active at a given time when the process starts from specified initial condition. Among many other applications, this task is crucial for a well-studied problem of influence maximization: finding optimal spreaders in a social network that maximize the influence spread by a certain time horizon. Indeed, influence estimation needs to be called multiple times for comparing candidate seed sets. Unfortunately, in many models of interest an exact computation of marginals is #P-hard. In practice, influence is often estimated using Monte-Carlo sampling methods that require a large number of runs for obtaining a high-fidelity prediction, especially at large times. It is thus desirable to develop analytic techniques as an alternative to sampling methods. Here, we suggest an algorithm for estimating the influence function in popular independent cascade model based on a scalable dynamic message-passing approach. This method has a computational complexity of a single Monte-Carlo simulation and provides an upper bound on the expected spread on a general graph, yielding exact answer for treelike networks. We also provide dynamic message-passing equations for a stochastic version of the linear threshold model. The resulting saving of a potentially large sampling factor in the running time compared to simulation-based techniques hence makes it possible to address large-scale problem instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge