Andrey Y. Lokhov
Efficient Learning of Lattice Gauge Theories with Fermions
Dec 22, 2025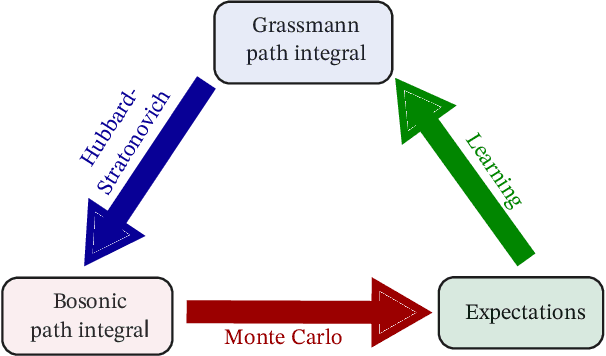
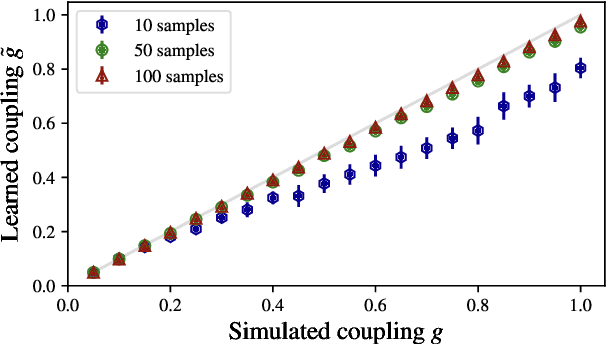
Abstract:We introduce a learning method for recovering action parameters in lattice field theories. Our method is based on the minimization of a convex loss function constructed using the Schwinger-Dyson relations. We show that score matching, a popular learning method, is a special case of our construction of an infinite family of valid loss functions. Importantly, our general Schwinger-Dyson-based construction applies to gauge theories and models with Grassmann-valued fields used to represent dynamical fermions. In particular, we extend our method to realistic lattice field theories including quantum chromodynamics.
Discrete distributions are learnable from metastable samples
Oct 17, 2024Abstract:Markov chain samplers designed to sample from multi-variable distributions often undesirably get stuck in specific regions of their state space. This causes such samplers to approximately sample from a metastable distribution which is usually quite different from the desired, stationary distribution of the chain. We show that single-variable conditionals of metastable distributions of reversible Markov chain samplers that satisfy a strong metastability condition are on average very close to those of the true distribution. This holds even when the metastable distribution is far away from the true model in terms of global metrics like Kullback-Leibler divergence or total variation distance. This property allows us to learn the true model using a conditional likelihood based estimator, even when the samples come from a metastable distribution concentrated in a small region of the state space. Explicit examples of such metastable states can be constructed from regions that effectively bottleneck the probability flow and cause poor mixing of the Markov chain. For specific cases of binary pairwise undirected graphical models, we extend our results to further rigorously show that data coming from metastable states can be used to learn the parameters of the energy function and recover the structure of the model.
Learning of networked spreading models from noisy and incomplete data
Dec 20, 2023Abstract:Recent years have seen a lot of progress in algorithms for learning parameters of spreading dynamics from both full and partial data. Some of the remaining challenges include model selection under the scenarios of unknown network structure, noisy data, missing observations in time, as well as an efficient incorporation of prior information to minimize the number of samples required for an accurate learning. Here, we introduce a universal learning method based on scalable dynamic message-passing technique that addresses these challenges often encountered in real data. The algorithm leverages available prior knowledge on the model and on the data, and reconstructs both network structure and parameters of a spreading model. We show that a linear computational complexity of the method with the key model parameters makes the algorithm scalable to large network instances.
Learning Energy-Based Representations of Quantum Many-Body States
Apr 08, 2023
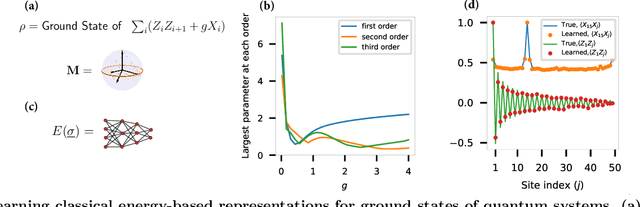

Abstract:Efficient representation of quantum many-body states on classical computers is a problem of enormous practical interest. An ideal representation of a quantum state combines a succinct characterization informed by the system's structure and symmetries, along with the ability to predict the physical observables of interest. A number of machine learning approaches have been recently used to construct such classical representations [1-6] which enable predictions of observables [7] and account for physical symmetries [8]. However, the structure of a quantum state gets typically lost unless a specialized ansatz is employed based on prior knowledge of the system [9-12]. Moreover, most such approaches give no information about what states are easier to learn in comparison to others. Here, we propose a new generative energy-based representation of quantum many-body states derived from Gibbs distributions used for modeling the thermal states of classical spin systems. Based on the prior information on a family of quantum states, the energy function can be specified by a small number of parameters using an explicit low-degree polynomial or a generic parametric family such as neural nets, and can naturally include the known symmetries of the system. Our results show that such a representation can be efficiently learned from data using exact algorithms in a form that enables the prediction of expectation values of physical observables. Importantly, the structure of the learned energy function provides a natural explanation for the hardness of learning for a given class of quantum states.
High-quality Thermal Gibbs Sampling with Quantum Annealing Hardware
Sep 03, 2021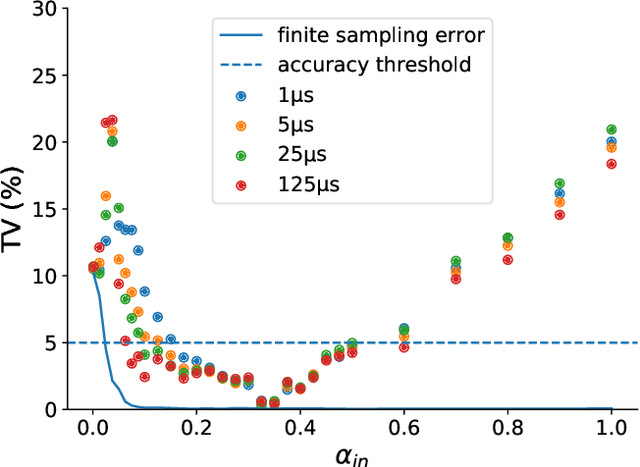
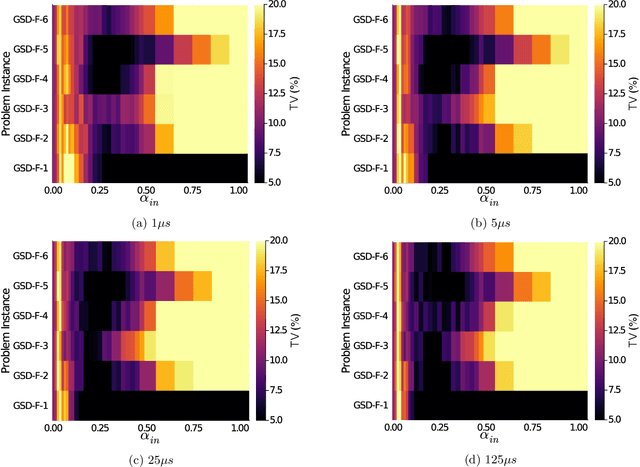
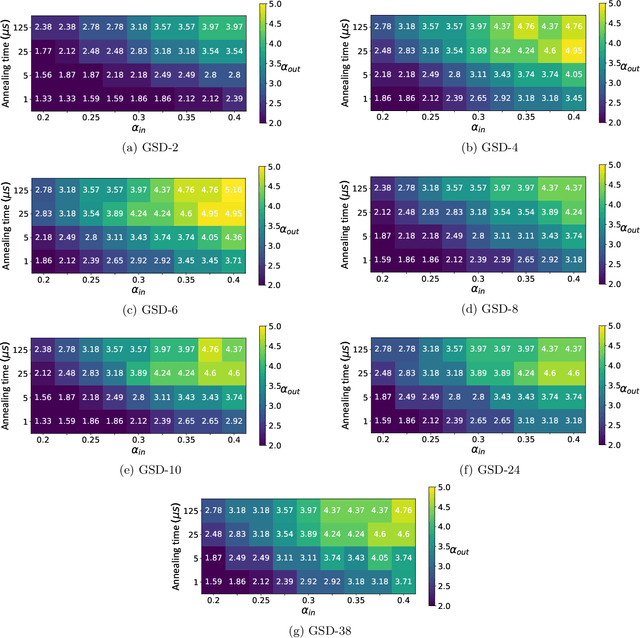
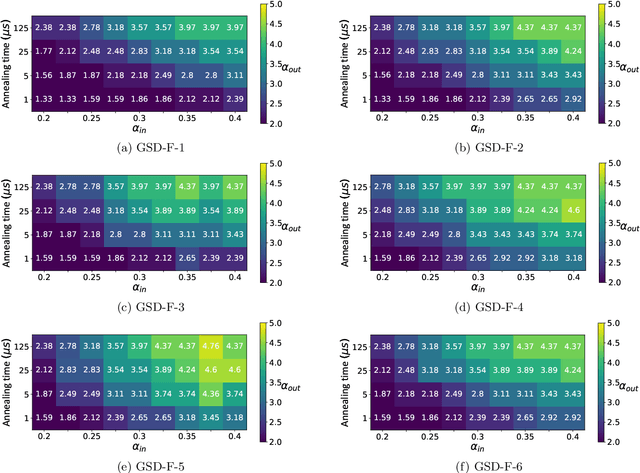
Abstract:Quantum Annealing (QA) was originally intended for accelerating the solution of combinatorial optimization tasks that have natural encodings as Ising models. However, recent experiments on QA hardware platforms have demonstrated that, in the operating regime corresponding to weak interactions, the QA hardware behaves like a noisy Gibbs sampler at a hardware-specific effective temperature. This work builds on those insights and identifies a class of small hardware-native Ising models that are robust to noise effects and proposes a novel procedure for executing these models on QA hardware to maximize Gibbs sampling performance. Experimental results indicate that the proposed protocol results in high-quality Gibbs samples from a hardware-specific effective temperature and that the QA annealing time can be used to adjust the effective temperature of the output distribution. The procedure proposed in this work provides a new approach to using QA hardware for Ising model sampling presenting potential new opportunities for applications in machine learning and physics simulation.
Single-Qubit Fidelity Assessment of Quantum Annealing Hardware
Apr 07, 2021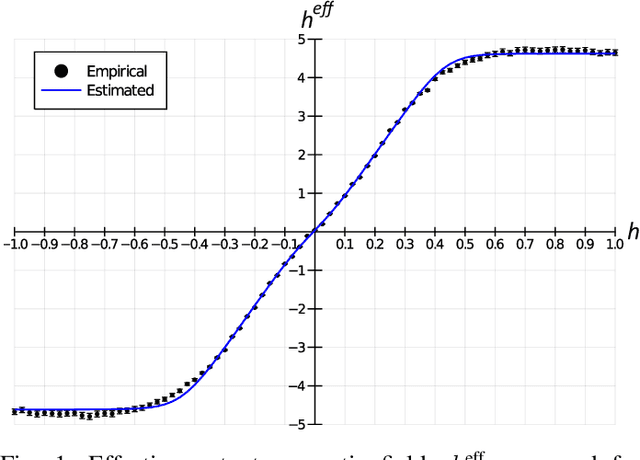
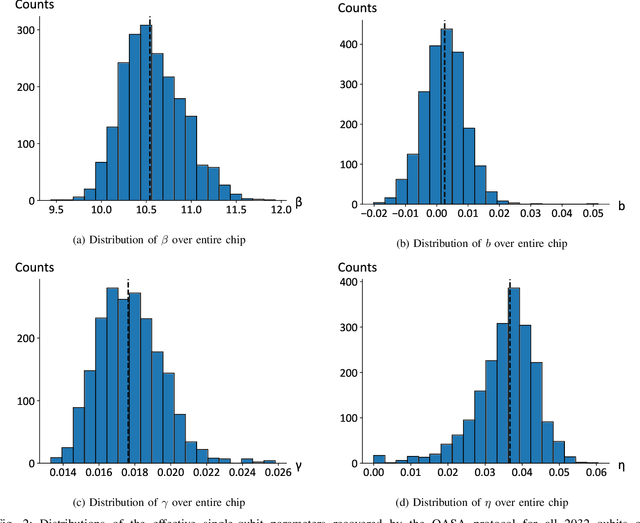
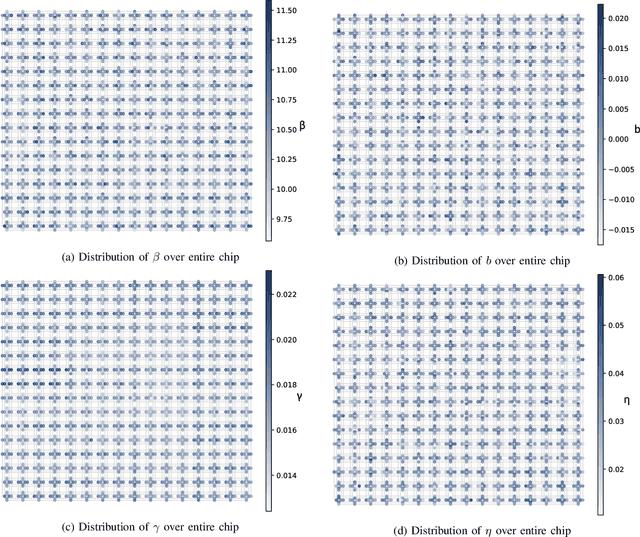
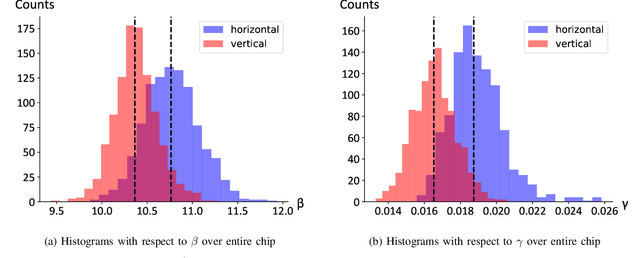
Abstract:As a wide variety of quantum computing platforms become available, methods for assessing and comparing the performance of these devices are of increasing interest and importance. Inspired by the success of single-qubit error rate computations for tracking the progress of gate-based quantum computers, this work proposes a Quantum Annealing Single-qubit Assessment (QASA) protocol for quantifying the performance of individual qubits in quantum annealing computers. The proposed protocol scales to large quantum annealers with thousands of qubits and provides unique insights into the distribution of qubit properties within a particular hardware device. The efficacy of the QASA protocol is demonstrated by analyzing the properties of a D-Wave 2000Q system, revealing unanticipated correlations in the qubit performance of that device. A study repeating the QASA protocol at different annealing times highlights how the method can be utilized to understand the impact of annealing parameters on qubit performance. Overall, the proposed QASA protocol provides a useful tool for assessing the performance of current and emerging quantum annealing devices.
Exponential Reduction in Sample Complexity with Learning of Ising Model Dynamics
Apr 02, 2021
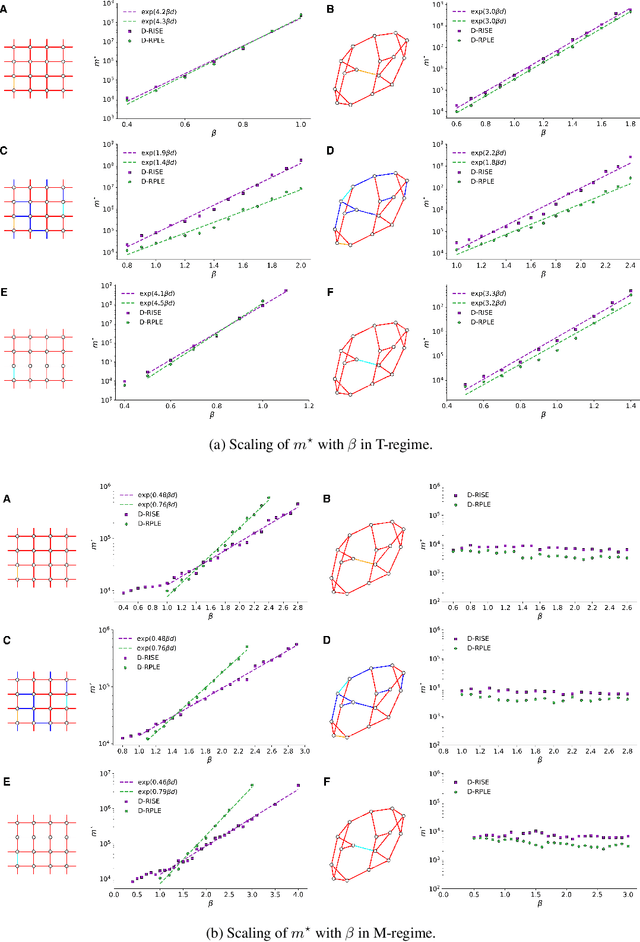
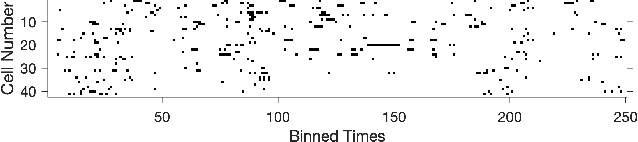
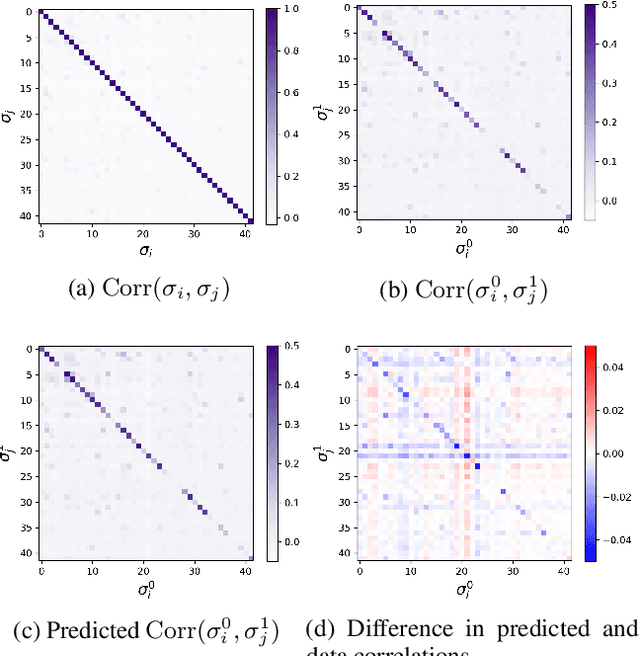
Abstract:The usual setting for learning the structure and parameters of a graphical model assumes the availability of independent samples produced from the corresponding multivariate probability distribution. However, for many models the mixing time of the respective Markov chain can be very large and i.i.d. samples may not be obtained. We study the problem of reconstructing binary graphical models from correlated samples produced by a dynamical process, which is natural in many applications. We analyze the sample complexity of two estimators that are based on the interaction screening objective and the conditional likelihood loss. We observe that for samples coming from a dynamical process far from equilibrium, the sample complexity reduces exponentially compared to a dynamical process that mixes quickly.
Learning Continuous Exponential Families Beyond Gaussian
Feb 18, 2021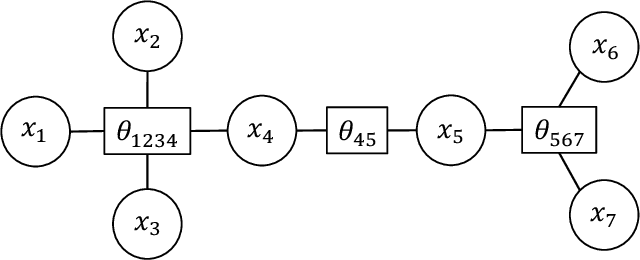
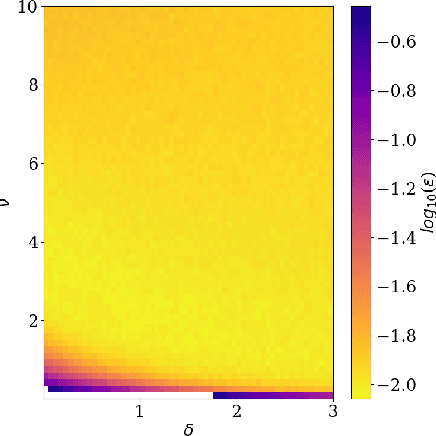
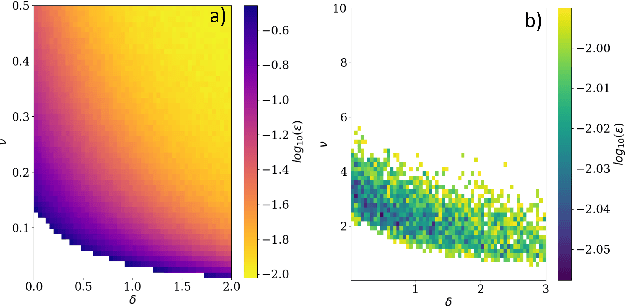
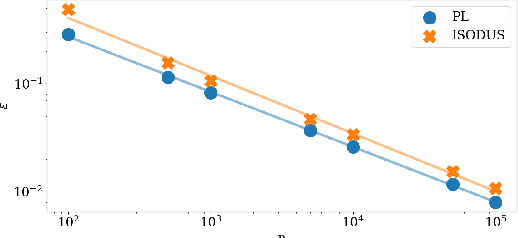
Abstract:We address the problem of learning of continuous exponential family distributions with unbounded support. While a lot of progress has been made on learning of Gaussian graphical models, we are still lacking scalable algorithms for reconstructing general continuous exponential families modeling higher-order moments of the data beyond the mean and the covariance. Here, we introduce a computationally efficient method for learning continuous graphical models based on the Interaction Screening approach. Through a series of numerical experiments, we show that our estimator maintains similar requirements in terms of accuracy and sample complexity compared to alternative approaches such as maximization of conditional likelihood, while considerably improving upon the algorithm's run-time.
Programmable Quantum Annealers as Noisy Gibbs Samplers
Dec 16, 2020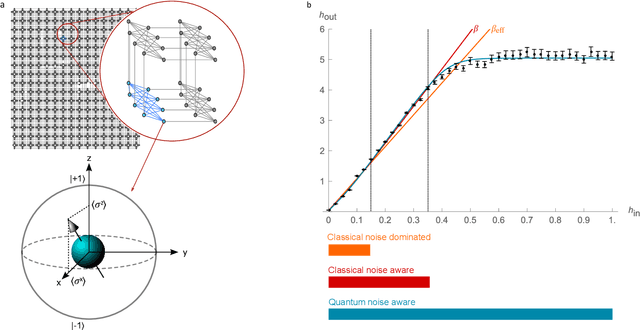
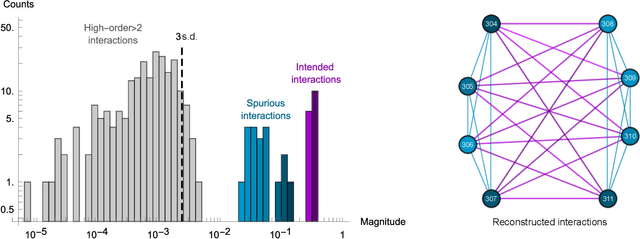
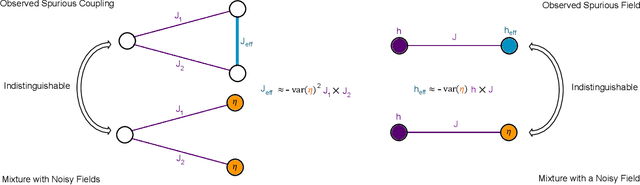
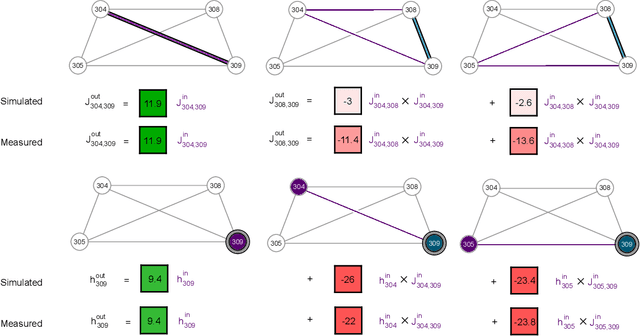
Abstract:Drawing independent samples from high-dimensional probability distributions represents the major computational bottleneck for modern algorithms, including powerful machine learning frameworks such as deep learning. The quest for discovering larger families of distributions for which sampling can be efficiently realized has inspired an exploration beyond established computing methods and turning to novel physical devices that leverage the principles of quantum computation. Quantum annealing embodies a promising computational paradigm that is intimately related to the complexity of energy landscapes in Gibbs distributions, which relate the probabilities of system states to the energies of these states. Here, we study the sampling properties of physical realizations of quantum annealers which are implemented through programmable lattices of superconducting flux qubits. Comprehensive statistical analysis of the data produced by these quantum machines shows that quantum annealers behave as samplers that generate independent configurations from low-temperature noisy Gibbs distributions. We show that the structure of the output distribution probes the intrinsic physical properties of the quantum device such as effective temperature of individual qubits and magnitude of local qubit noise, which result in a non-linear response function and spurious interactions that are absent in the hardware implementation. We anticipate that our methodology will find widespread use in characterization of future generations of quantum annealers and other emerging analog computing devices.
Scalable Learning of Independent Cascade Dynamics from Partial Observations
Jul 13, 2020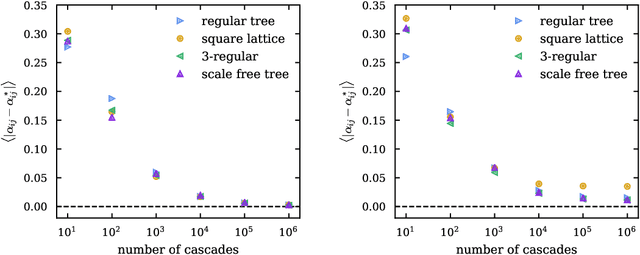
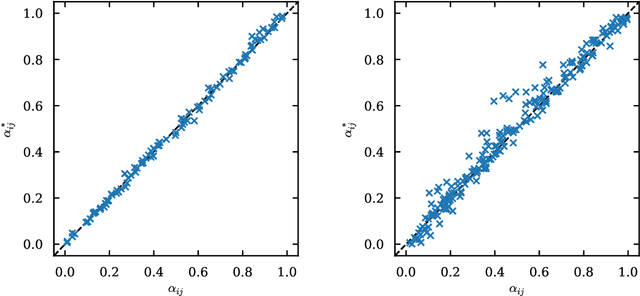
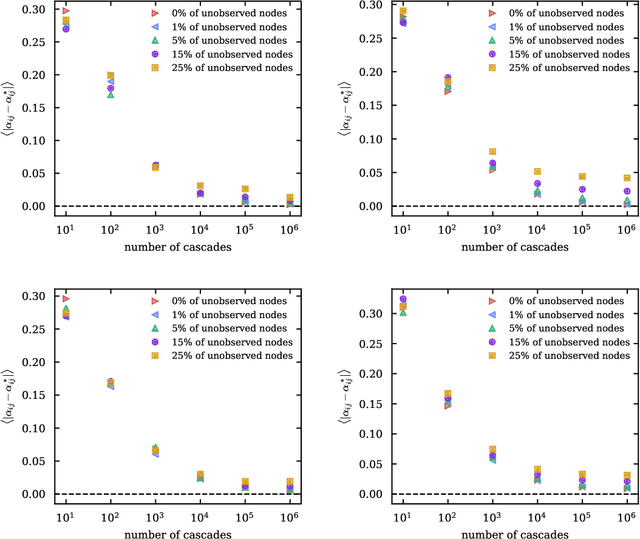
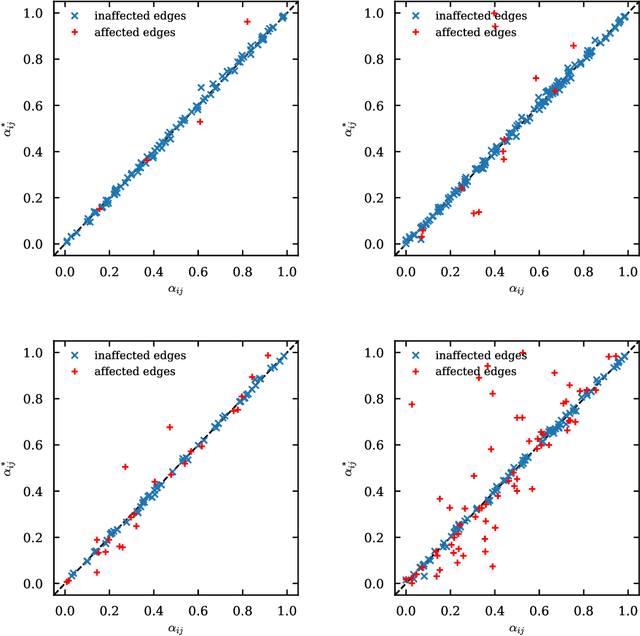
Abstract:Spreading processes play an increasingly important role in modeling for diffusion networks, information propagation, marketing, and opinion setting. Recent real-world spreading events further highlight the need for prediction, optimization, and control of diffusion dynamics. To tackle these tasks, it is essential to learn the effective spreading model and transmission probabilities across the network of interactions. However, in most cases the transmission rates are unknown and need to be inferred from the spreading data. Additionally, full observation of the dynamics is rarely available. As a result, standard approaches such as maximum likelihood quickly become intractable for large network instances. In this work, we study the popular Independent Cascade model of stochastic diffusion dynamics. We introduce a computationally efficient algorithm, based on a scalable dynamic message-passing approach, which is able to learn parameters of the effective spreading model given only limited information on the activation times of nodes in the network. Importantly, we show that the resulting model approximates the marginal activation probabilities that can be used for prediction of the spread.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge