Discrete Diffusion with Sample-Efficient Estimators for Conditionals

We study a discrete denoising diffusion framework that integrates a sample-efficient estimator of single-site conditionals with round-robin noising and denoising dynamics for generative modeling over discrete state spaces. Rather than approximating a discrete analog of a score function, our formulation treats single-site conditional probabilities as the fundamental objects that parameterize the reverse diffusion process. We employ a sample-efficient method known as Neural Interaction Screening Estimator (NeurISE) to estimate these conditionals in the diffusion dynamics. Controlled experiments on synthetic Ising models, MNIST, and scientific data sets produced by a D-Wave quantum annealer, synthetic Potts model and one-dimensional quantum systems demonstrate the proposed approach. On the binary data sets, these experiments demonstrate that the proposed approach outperforms popular existing methods including ratio-based approaches, achieving improved performance in total variation, cross-correlations, and kernel density estimation metrics.

Computationally sufficient statistics for Ising models

Learning Gibbs distributions using only sufficient statistics has long been recognized as a computationally hard problem. On the other hand, computationally efficient algorithms for learning Gibbs distributions rely on access to full sample configurations generated from the model. For many systems of interest that arise in physical contexts, expecting a full sample to be observed is not practical, and hence it is important to look for computationally efficient methods that solve the learning problem with access to only a limited set of statistics. We examine the trade-offs between the power of computation and observation within this scenario, employing the Ising model as a paradigmatic example. We demonstrate that it is feasible to reconstruct the model parameters for a model with $\ell_1$ width $γ$ by observing statistics up to an order of $O(γ)$. This approach allows us to infer the model's structure and also learn its couplings and magnetic fields. We also discuss a setting where prior information about structure of the model is available and show that the learning problem can be solved efficiently with even more limited observational power.

Efficient Learning of Lattice Gauge Theories with Fermions

We introduce a learning method for recovering action parameters in lattice field theories. Our method is based on the minimization of a convex loss function constructed using the Schwinger-Dyson relations. We show that score matching, a popular learning method, is a special case of our construction of an infinite family of valid loss functions. Importantly, our general Schwinger-Dyson-based construction applies to gauge theories and models with Grassmann-valued fields used to represent dynamical fermions. In particular, we extend our method to realistic lattice field theories including quantum chromodynamics.

Discrete distributions are learnable from metastable samples

Markov chain samplers designed to sample from multi-variable distributions often undesirably get stuck in specific regions of their state space. This causes such samplers to approximately sample from a metastable distribution which is usually quite different from the desired, stationary distribution of the chain. We show that single-variable conditionals of metastable distributions of reversible Markov chain samplers that satisfy a strong metastability condition are on average very close to those of the true distribution. This holds even when the metastable distribution is far away from the true model in terms of global metrics like Kullback-Leibler divergence or total variation distance. This property allows us to learn the true model using a conditional likelihood based estimator, even when the samples come from a metastable distribution concentrated in a small region of the state space. Explicit examples of such metastable states can be constructed from regions that effectively bottleneck the probability flow and cause poor mixing of the Markov chain. For specific cases of binary pairwise undirected graphical models, we extend our results to further rigorously show that data coming from metastable states can be used to learn the parameters of the energy function and recover the structure of the model.

Learning Energy-Based Representations of Quantum Many-Body States

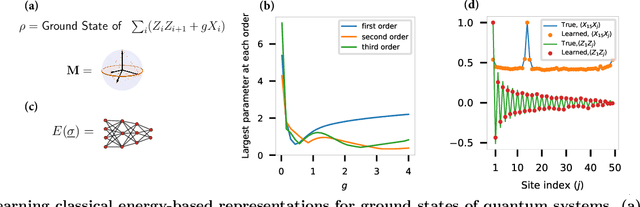
Efficient representation of quantum many-body states on classical computers is a problem of enormous practical interest. An ideal representation of a quantum state combines a succinct characterization informed by the system's structure and symmetries, along with the ability to predict the physical observables of interest. A number of machine learning approaches have been recently used to construct such classical representations [1-6] which enable predictions of observables [7] and account for physical symmetries [8]. However, the structure of a quantum state gets typically lost unless a specialized ansatz is employed based on prior knowledge of the system [9-12]. Moreover, most such approaches give no information about what states are easier to learn in comparison to others. Here, we propose a new generative energy-based representation of quantum many-body states derived from Gibbs distributions used for modeling the thermal states of classical spin systems. Based on the prior information on a family of quantum states, the energy function can be specified by a small number of parameters using an explicit low-degree polynomial or a generic parametric family such as neural nets, and can naturally include the known symmetries of the system. Our results show that such a representation can be efficiently learned from data using exact algorithms in a form that enables the prediction of expectation values of physical observables. Importantly, the structure of the learned energy function provides a natural explanation for the hardness of learning for a given class of quantum states.