Learning of networked spreading models from noisy and incomplete data

Recent years have seen a lot of progress in algorithms for learning parameters of spreading dynamics from both full and partial data. Some of the remaining challenges include model selection under the scenarios of unknown network structure, noisy data, missing observations in time, as well as an efficient incorporation of prior information to minimize the number of samples required for an accurate learning. Here, we introduce a universal learning method based on scalable dynamic message-passing technique that addresses these challenges often encountered in real data. The algorithm leverages available prior knowledge on the model and on the data, and reconstructs both network structure and parameters of a spreading model. We show that a linear computational complexity of the method with the key model parameters makes the algorithm scalable to large network instances.

Scalable Learning of Independent Cascade Dynamics from Partial Observations

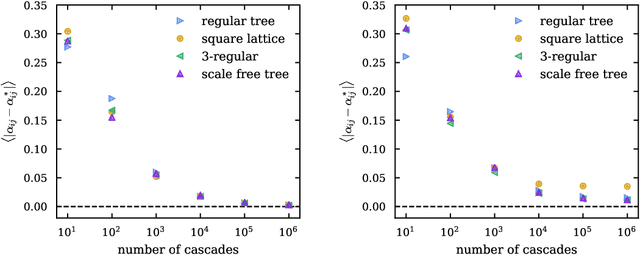
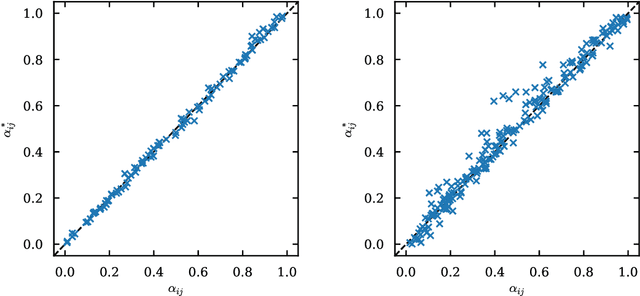
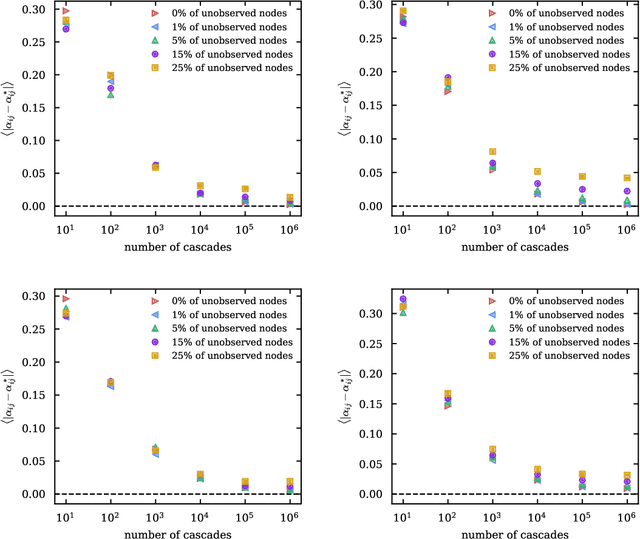
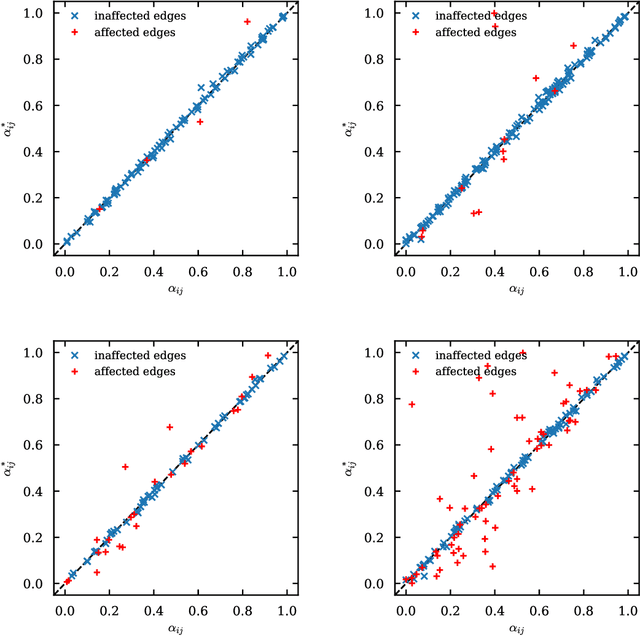
Spreading processes play an increasingly important role in modeling for diffusion networks, information propagation, marketing, and opinion setting. Recent real-world spreading events further highlight the need for prediction, optimization, and control of diffusion dynamics. To tackle these tasks, it is essential to learn the effective spreading model and transmission probabilities across the network of interactions. However, in most cases the transmission rates are unknown and need to be inferred from the spreading data. Additionally, full observation of the dynamics is rarely available. As a result, standard approaches such as maximum likelihood quickly become intractable for large network instances. In this work, we study the popular Independent Cascade model of stochastic diffusion dynamics. We introduce a computationally efficient algorithm, based on a scalable dynamic message-passing approach, which is able to learn parameters of the effective spreading model given only limited information on the activation times of nodes in the network. Importantly, we show that the resulting model approximates the marginal activation probabilities that can be used for prediction of the spread.