The Space of Functions Computed by Deep Layered Machines
Paper and Code
May 21, 2020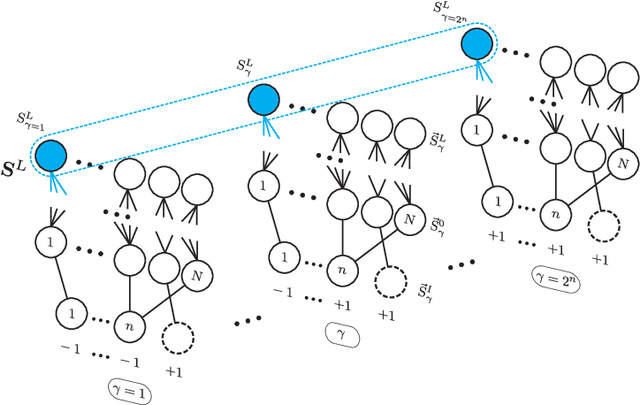
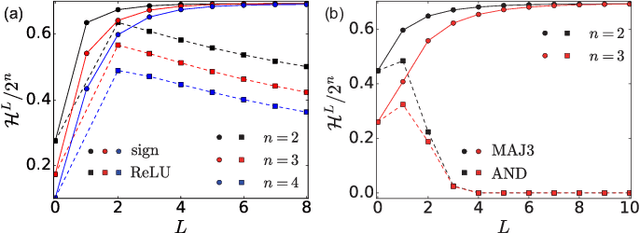
We study the space of functions computed by random layered machines, including deep neural networks, and Boolean circuits. Investigating the distribution of Boolean functions computed on the recurrent and layer-dependent architectures, we find that it is the same in both models. Depending on the initial conditions and computing elements used, we characterize the space of functions computed at the large depth limit and show that the macroscopic entropy of Boolean functions is either monotonically increasing or decreasing with the growing depth.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge