Adaptive Resampling with Bootstrap for Noisy Multi-Objective Optimization Problems

The challenge of noisy multi-objective optimization lies in the constant trade-off between exploring new decision points and improving the precision of known points through resampling. This decision should take into account both the variability of the objective functions and the current estimate of a point in relation to the Pareto front. Since the amount and distribution of noise are generally unknown, it is desirable for a decision function to be highly adaptive to the properties of the optimization problem. This paper presents a resampling decision function that incorporates the stochastic nature of the optimization problem by using bootstrapping and the probability of dominance. The distribution-free estimation of the probability of dominance is achieved using bootstrap estimates of the means. To make the procedure applicable even with very few observations, we transfer the distribution observed at other decision points. The efficiency of this resampling approach is demonstrated by applying it in the NSGA-II algorithm with a sequential resampling procedure under multiple noise variations.

RODD: Robust Outlier Detection in Data Cubes

Data cubes are multidimensional databases, often built from several separate databases, that serve as flexible basis for data analysis. Surprisingly, outlier detection on data cubes has not yet been treated extensively. In this work, we provide the first framework to evaluate robust outlier detection methods in data cubes (RODD). We introduce a novel random forest-based outlier detection approach (RODD-RF) and compare it with more traditional methods based on robust location estimators. We propose a general type of test data and examine all methods in a simulation study. Moreover, we apply ROOD-RF to real world data. The results show that RODD-RF can lead to improved outlier detection.

Using Sequential Statistical Tests to Improve the Performance of Random Search in hyperparameter Tuning

Hyperparamter tuning is one of the the most time-consuming parts in machine learning: The performance of a large number of different hyperparameter settings has to be evaluated to find the best one. Although modern optimization algorithms exist that minimize the number of evaluations needed, the evaluation of a single setting is still expensive: Using a resampling technique, the machine learning method has to be fitted a fixed number of $K$ times on different training data sets. As an estimator for the performance of the setting the respective mean value of the $K$ fits is used. Many hyperparameter settings could be discarded after less than $K$ resampling iterations, because they already are clearly inferior to high performing settings. However, in practice, the resampling is often performed until the very end, wasting a lot of computational effort. We propose to use a sequential testing procedure to minimize the number of resampling iterations to detect inferior parameter setting. To do so, we first analyze the distribution of resampling errors, we will find out, that a log-normal distribution is promising. Afterwards, we build a sequential testing procedure assuming this distribution. This sequential test procedure is utilized within a random search algorithm. We compare a standard random search with our enhanced sequential random search in some realistic data situation. It can be shown that the sequential random search is able to find comparably good hyperparameter settings, however, the computational time needed to find those settings is roughly halved.

Random boosting and random^2 forests -- A random tree depth injection approach

The induction of additional randomness in parallel and sequential ensemble methods has proven to be worthwhile in many aspects. In this manuscript, we propose and examine a novel random tree depth injection approach suitable for sequential and parallel tree-based approaches including Boosting and Random Forests. The resulting methods are called \emph{Random Boost} and \emph{Random$^2$ Forest}. Both approaches serve as valuable extensions to the existing literature on the gradient boosting framework and random forests. A Monte Carlo simulation, in which tree-shaped data sets with different numbers of final partitions are built, suggests that there are several scenarios where \emph{Random Boost} and \emph{Random$^2$ Forest} can improve the prediction performance of conventional hierarchical boosting and random forest approaches. The new algorithms appear to be especially successful in cases where there are merely a few high-order interactions in the generated data. In addition, our simulations suggest that our random tree depth injection approach can improve computation time by up to 40%, while at the same time the performance losses in terms of prediction accuracy turn out to be minor or even negligible in most cases.

A First Analysis of Kernels for Kriging-based Optimization in Hierarchical Search Spaces

Many real-world optimization problems require significant resources for objective function evaluations. This is a challenge to evolutionary algorithms, as it limits the number of available evaluations. One solution are surrogate models, which replace the expensive objective. A particular issue in this context are hierarchical variables. Hierarchical variables only influence the objective function if other variables satisfy some condition. We study how this kind of hierarchical structure can be integrated into the model based optimization framework. We discuss an existing kernel and propose alternatives. An artificial test function is used to investigate how different kernels and assumptions affect model quality and search performance.

mlrMBO: A Modular Framework for Model-Based Optimization of Expensive Black-Box Functions

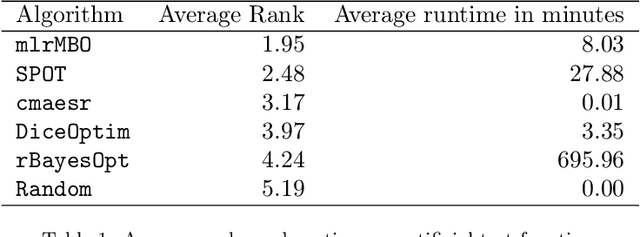
We present mlrMBO, a flexible and comprehensive R toolbox for model-based optimization (MBO), also known as Bayesian optimization, which addresses the problem of expensive black-box optimization by approximating the given objective function through a surrogate regression model. It is designed for both single- and multi-objective optimization with mixed continuous, categorical and conditional parameters. Additional features include multi-point batch proposal, parallelization, visualization, logging and error-handling. mlrMBO is implemented in a modular fashion, such that single components can be easily replaced or adapted by the user for specific use cases, e.g., any regression learner from the mlr toolbox for machine learning can be used, and infill criteria and infill optimizers are easily exchangeable. We empirically demonstrate that mlrMBO provides state-of-the-art performance by comparing it on different benchmark scenarios against a wide range of other optimizers, including DiceOptim, rBayesianOptimization, SPOT, SMAC, Spearmint, and Hyperopt.

Fast model selection by limiting SVM training times

Kernelized Support Vector Machines (SVMs) are among the best performing supervised learning methods. But for optimal predictive performance, time-consuming parameter tuning is crucial, which impedes application. To tackle this problem, the classic model selection procedure based on grid-search and cross-validation was refined, e.g. by data subsampling and direct search heuristics. Here we focus on a different aspect, the stopping criterion for SVM training. We show that by limiting the training time given to the SVM solver during parameter tuning we can reduce model selection times by an order of magnitude.