Thi Ngoc Tien Tran
Random boosting and random^2 forests -- A random tree depth injection approach
Sep 13, 2020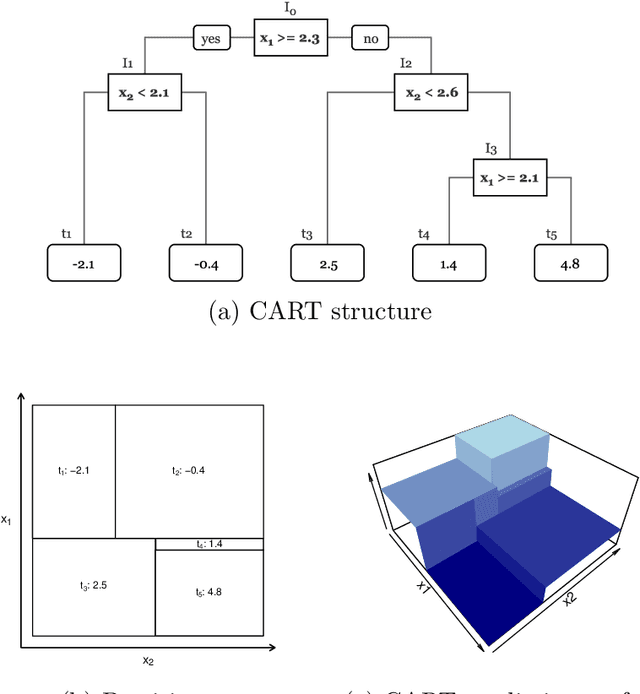
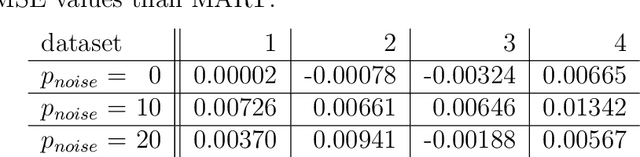
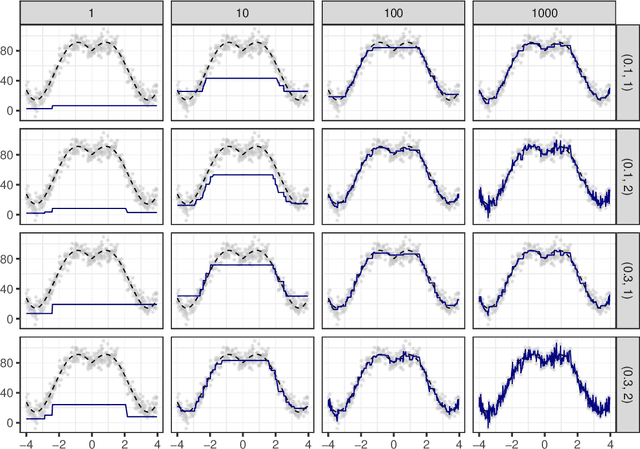
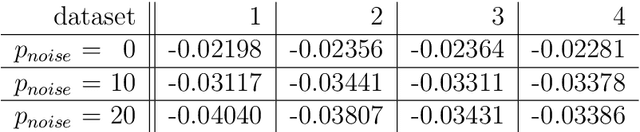
Abstract:The induction of additional randomness in parallel and sequential ensemble methods has proven to be worthwhile in many aspects. In this manuscript, we propose and examine a novel random tree depth injection approach suitable for sequential and parallel tree-based approaches including Boosting and Random Forests. The resulting methods are called \emph{Random Boost} and \emph{Random$^2$ Forest}. Both approaches serve as valuable extensions to the existing literature on the gradient boosting framework and random forests. A Monte Carlo simulation, in which tree-shaped data sets with different numbers of final partitions are built, suggests that there are several scenarios where \emph{Random Boost} and \emph{Random$^2$ Forest} can improve the prediction performance of conventional hierarchical boosting and random forest approaches. The new algorithms appear to be especially successful in cases where there are merely a few high-order interactions in the generated data. In addition, our simulations suggest that our random tree depth injection approach can improve computation time by up to 40%, while at the same time the performance losses in terms of prediction accuracy turn out to be minor or even negligible in most cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge