Lifted Variable Elimination: Decoupling the Operators from the Constraint Language

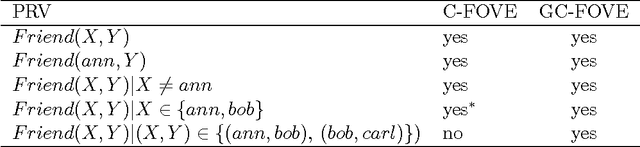
Lifted probabilistic inference algorithms exploit regularities in the structure of graphical models to perform inference more efficiently. More specifically, they identify groups of interchangeable variables and perform inference once per group, as opposed to once per variable. The groups are defined by means of constraints, so the flexibility of the grouping is determined by the expressivity of the constraint language. Existing approaches for exact lifted inference use specific languages for (in)equality constraints, which often have limited expressivity. In this article, we decouple lifted inference from the constraint language. We define operators for lifted inference in terms of relational algebra operators, so that they operate on the semantic level (the constraints extension) rather than on the syntactic level, making them language-independent. As a result, lifted inference can be performed using more powerful constraint languages, which provide more opportunities for lifting. We empirically demonstrate that this can improve inference efficiency by orders of magnitude, allowing exact inference where until now only approximate inference was feasible.

Inference and learning in probabilistic logic programs using weighted Boolean formulas

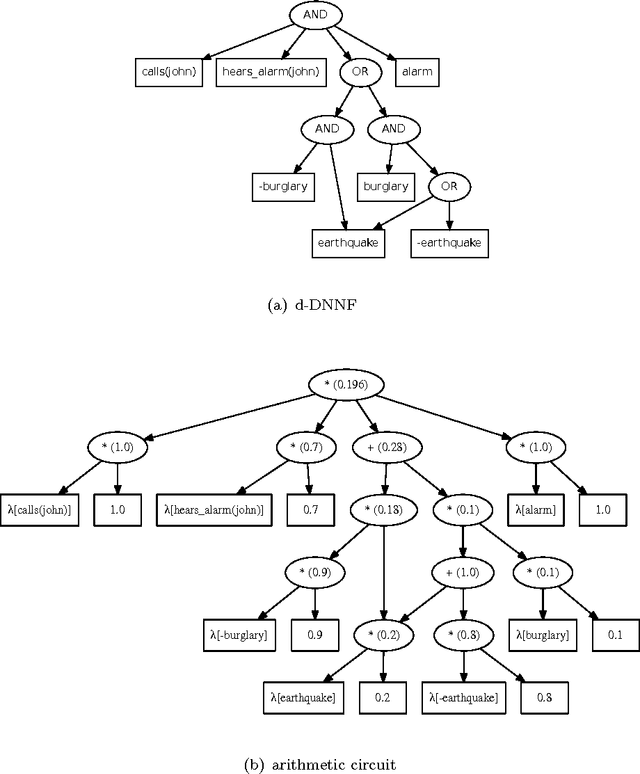
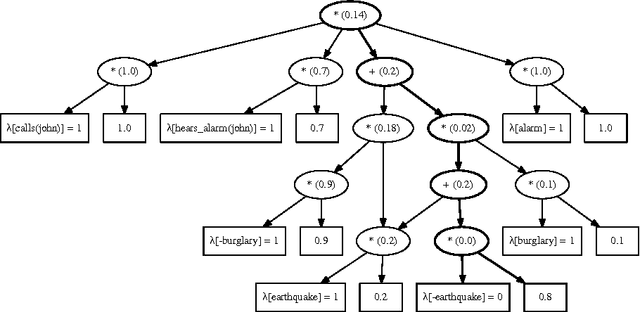
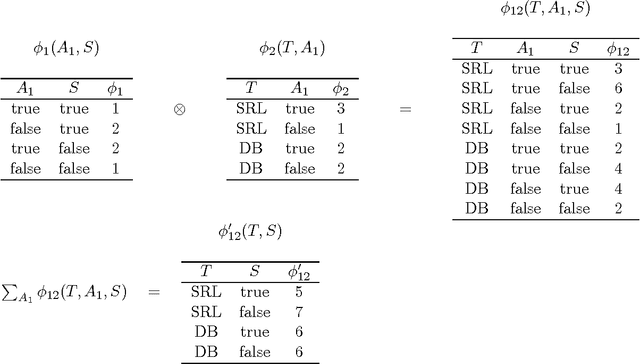
Probabilistic logic programs are logic programs in which some of the facts are annotated with probabilities. This paper investigates how classical inference and learning tasks known from the graphical model community can be tackled for probabilistic logic programs. Several such tasks such as computing the marginals given evidence and learning from (partial) interpretations have not really been addressed for probabilistic logic programs before. The first contribution of this paper is a suite of efficient algorithms for various inference tasks. It is based on a conversion of the program and the queries and evidence to a weighted Boolean formula. This allows us to reduce the inference tasks to well-studied tasks such as weighted model counting, which can be solved using state-of-the-art methods known from the graphical model and knowledge compilation literature. The second contribution is an algorithm for parameter estimation in the learning from interpretations setting. The algorithm employs Expectation Maximization, and is built on top of the developed inference algorithms. The proposed approach is experimentally evaluated. The results show that the inference algorithms improve upon the state-of-the-art in probabilistic logic programming and that it is indeed possible to learn the parameters of a probabilistic logic program from interpretations.

Lifted Variable Elimination: A Novel Operator and Completeness Results

Various methods for lifted probabilistic inference have been proposed, but our understanding of these methods and the relationships between them is still limited, compared to their propositional counterparts. The only existing theoretical characterization of lifting is for weighted first-order model counting (WFOMC), which was shown to be complete domain-lifted for the class of 2-logvar models. This paper makes two contributions to lifted variable elimination (LVE). First, we introduce a novel inference operator called group inversion. Second, we prove that LVE augmented with this operator is complete in the same sense as WFOMC.

Inference in Probabilistic Logic Programs using Weighted CNF's

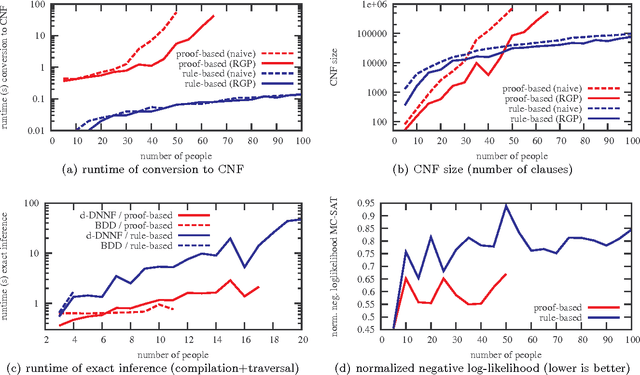
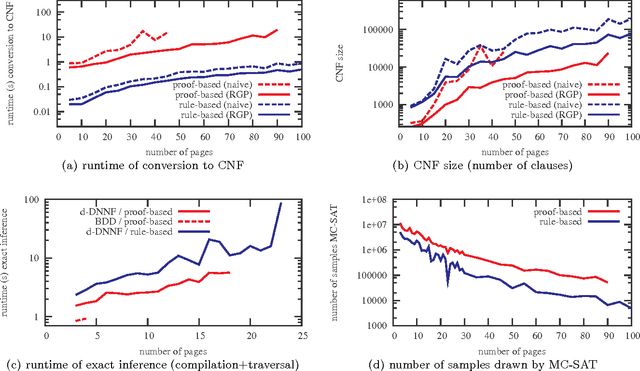
Probabilistic logic programs are logic programs in which some of the facts are annotated with probabilities. Several classical probabilistic inference tasks (such as MAP and computing marginals) have not yet received a lot of attention for this formalism. The contribution of this paper is that we develop efficient inference algorithms for these tasks. This is based on a conversion of the probabilistic logic program and the query and evidence to a weighted CNF formula. This allows us to reduce the inference tasks to well-studied tasks such as weighted model counting. To solve such tasks, we employ state-of-the-art methods. We consider multiple methods for the conversion of the programs as well as for inference on the weighted CNF. The resulting approach is evaluated experimentally and shown to improve upon the state-of-the-art in probabilistic logic programming.

Improving the Efficiency of Approximate Inference for Probabilistic Logical Models by means of Program Specialization

We consider the task of performing probabilistic inference with probabilistic logical models. Many algorithms for approximate inference with such models are based on sampling. From a logic programming perspective, sampling boils down to repeatedly calling the same queries on a knowledge base composed of a static part and a dynamic part. The larger the static part, the more redundancy there is in these repeated calls. This is problematic since inefficient sampling yields poor approximations. We show how to apply logic program specialization to make sampling-based inference more efficient. We develop an algorithm that specializes the definitions of the query predicates with respect to the static part of the knowledge base. In experiments on real-world data we obtain speedups of up to an order of magnitude, and these speedups grow with the data-size.