Nima Taghipour
Lifted Variable Elimination: Decoupling the Operators from the Constraint Language
Feb 04, 2014
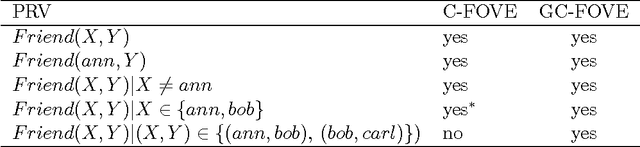
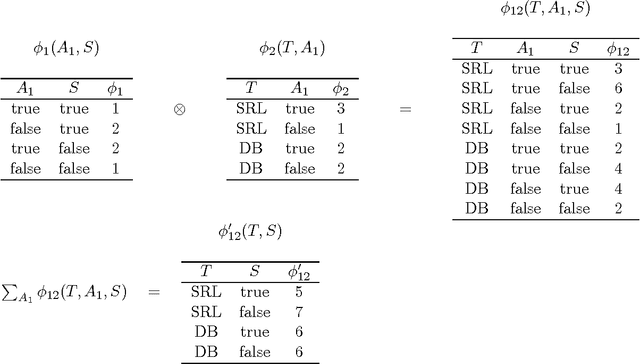

Abstract:Lifted probabilistic inference algorithms exploit regularities in the structure of graphical models to perform inference more efficiently. More specifically, they identify groups of interchangeable variables and perform inference once per group, as opposed to once per variable. The groups are defined by means of constraints, so the flexibility of the grouping is determined by the expressivity of the constraint language. Existing approaches for exact lifted inference use specific languages for (in)equality constraints, which often have limited expressivity. In this article, we decouple lifted inference from the constraint language. We define operators for lifted inference in terms of relational algebra operators, so that they operate on the semantic level (the constraints extension) rather than on the syntactic level, making them language-independent. As a result, lifted inference can be performed using more powerful constraint languages, which provide more opportunities for lifting. We empirically demonstrate that this can improve inference efficiency by orders of magnitude, allowing exact inference where until now only approximate inference was feasible.
First-Order Decomposition Trees
Jun 04, 2013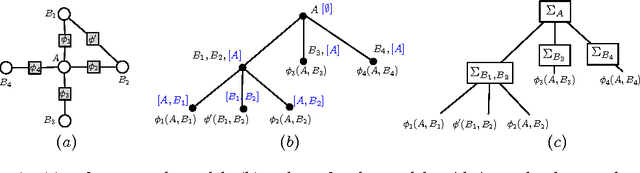

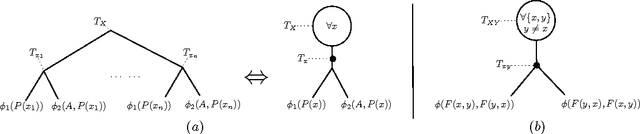

Abstract:Lifting attempts to speed up probabilistic inference by exploiting symmetries in the model. Exact lifted inference methods, like their propositional counterparts, work by recursively decomposing the model and the problem. In the propositional case, there exist formal structures, such as decomposition trees (dtrees), that represent such a decomposition and allow us to determine the complexity of inference a priori. However, there is currently no equivalent structure nor analogous complexity results for lifted inference. In this paper, we introduce FO-dtrees, which upgrade propositional dtrees to the first-order level. We show how these trees can characterize a lifted inference solution for a probabilistic logical model (in terms of a sequence of lifted operations), and make a theoretical analysis of the complexity of lifted inference in terms of the novel notion of lifted width for the tree.
Lifted Variable Elimination: A Novel Operator and Completeness Results
Aug 24, 2012
Abstract:Various methods for lifted probabilistic inference have been proposed, but our understanding of these methods and the relationships between them is still limited, compared to their propositional counterparts. The only existing theoretical characterization of lifting is for weighted first-order model counting (WFOMC), which was shown to be complete domain-lifted for the class of 2-logvar models. This paper makes two contributions to lifted variable elimination (LVE). First, we introduce a novel inference operator called group inversion. Second, we prove that LVE augmented with this operator is complete in the same sense as WFOMC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge