Lifted Variable Elimination: Decoupling the Operators from the Constraint Language
Paper and Code
Feb 04, 2014
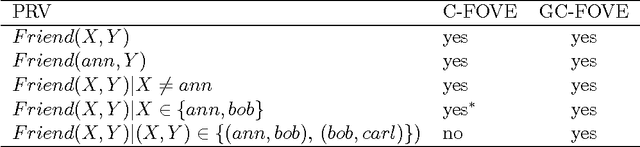
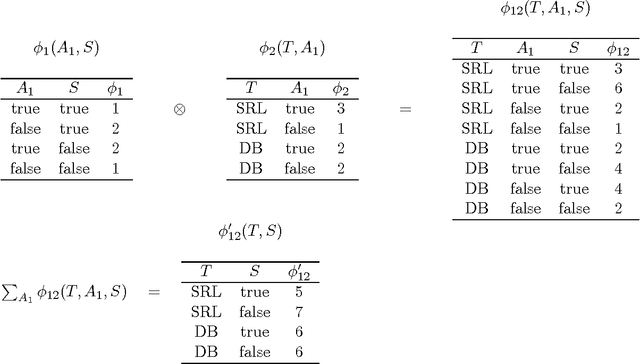

Lifted probabilistic inference algorithms exploit regularities in the structure of graphical models to perform inference more efficiently. More specifically, they identify groups of interchangeable variables and perform inference once per group, as opposed to once per variable. The groups are defined by means of constraints, so the flexibility of the grouping is determined by the expressivity of the constraint language. Existing approaches for exact lifted inference use specific languages for (in)equality constraints, which often have limited expressivity. In this article, we decouple lifted inference from the constraint language. We define operators for lifted inference in terms of relational algebra operators, so that they operate on the semantic level (the constraints extension) rather than on the syntactic level, making them language-independent. As a result, lifted inference can be performed using more powerful constraint languages, which provide more opportunities for lifting. We empirically demonstrate that this can improve inference efficiency by orders of magnitude, allowing exact inference where until now only approximate inference was feasible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge