Unsupervised Identification and Removal of Spurious Correlations During Fine-Tuning

Fine-tuning a pretrained language model on a curated dataset can produce spurious correlations between the fine-tuning task and unintended latent factors -- such as misaligned personas or political slant -- that the curation procedure has entangled with the task. The model can latch onto these spurious correlations, leading to bias and reduced out-of-distribution generalisation. We prove that under reasonable assumptions on task complexity and the spurious correlation, such latent factors can be identified, without supervision, from the weights of a naive LoRA fine-tune. Existing approaches to removing bias, such as activation steering, remove identified factors from residual-stream activations, either at inference or during training. We argue, however, that the goal should be to remove the spurious correlation, not the latent factor itself, as the pretrained model may rely on it for genuine task signal. To enable this, we propose GRASP, GRadient projection of Associated Spurious Patterns, which prevents the model from acquiring new reliance on the identified latent factor while preserving any pretrained content along it. We validate on three fine-tuning tasks. The first two involve emergent misalignment, where fine-tuning on a narrow task -- in our case, writing insecure code and giving bad medical advice -- leads to misaligned responses on unrelated topics. Here our method completely removes misalignment in the insecure code case and reduces them by ~5x in the bad medical advice case, beating all baselines in the trade-off between misalignment-reduction and task-preservation. The last is a novel political-bias experiment, where fine-tuning on right-skewed Reddit financial-advice data causes political-lean drift on unrelated topics. Here our method reduces drift by more than half, while improving financial task performance, beating all baselines.

Causal Representation Learning for Generalisable Recommendation

Predictive models trained on observational data often fail to generalise to the distributions they encounter when deployed, especially when the training data is a product of the system being optimised. Recommender systems are a canonical example: they are trained on interaction logs confounded by the deployed policy, past user behaviour, and platform filtering. As a result, the training distribution differs substantially from the candidate distribution scored at serving time, a gap that makes offline metrics unreliable predictors of online performance. We address the distribution shift problem with a method motivated by causal representation learning (CRL). We propose an information-theoretic disentanglement criterion and prove that its optimum depends only on the causal components of the input. We then derive a tractable variational lower bound that makes the criterion optimisable from finite observational data alone. The scope of our method is narrower than that of much of the CRL literature, in that we target better generalisation under distribution shift, not full identification of all latent causal factors. This narrower target is what makes the method practical, requiring only the existing confounded logs, applying to any standard supervised model, and adding no inference-time cost. Our headline evaluation is an A/B test with millions of users on Spotify, applied to a production ranker for personalised playlist generation. A capacity-matched CRL variant performed on par offline but delivered substantial online gains in listener engagement. Complementary evidence on the public KuaiRand recommendation dataset and a synthetic benchmark with known causal structure shows the same pattern: offline parity with baseline, gains under distribution shift. Across all three settings, adding our causal disentanglement objective yields meaningfully better out-of-distribution generalisation.

Quantum oracles give an advantage for identifying classical counterfactuals

We show that quantum oracles provide an advantage over classical oracles for answering classical counterfactual questions in causal models, or equivalently, for identifying unknown causal parameters such as distributions over functional dependences. In structural causal models with discrete classical variables, observational data and even ideal interventions generally fail to answer all counterfactual questions, since different causal parameters can reproduce the same observational and interventional data while disagreeing on counterfactuals. Using a simple binary example, we demonstrate that if the classical variables of interest are encoded in quantum systems and the causal dependence among them is encoded in a quantum oracle, coherently querying the oracle enables the identification of all causal parameters -- hence all classical counterfactuals. We generalize this to arbitrary finite cardinalities and prove that coherent probing 1) allows the identification of all two-way joint counterfactuals p(Y_x=y, Y_{x'}=y'), which is not possible with any number of queries to a classical oracle, and 2) provides tighter bounds on higher-order multi-way counterfactuals than with a classical oracle. This work can also be viewed as an extension to traditional quantum oracle problems such as Deutsch--Jozsa to identifying more causal parameters beyond just, e.g., whether a function is constant or balanced. Finally, we raise the question of whether this quantum advantage relies on uniquely non-classical features like contextuality. We provide some evidence against this by showing that in the binary case, oracles in some classically-explainable theories like Spekkens' toy theory also give rise to a counterfactual identifiability advantage over strictly classical oracles.

Local Interference: Removing Interference Bias in Semi-Parametric Causal Models

Interference bias is a major impediment to identifying causal effects in real-world settings. For example, vaccination reduces the transmission of a virus in a population such that everyone benefits -- even those who are not treated. This is a source of bias that must be accounted for if one wants to learn the true effect of a vaccine on an individual's immune system. Previous approaches addressing interference bias require strong domain knowledge in the form of a graphical interaction network fully describing interference between units. Moreover, they place additional constraints on the form the interference can take, such as restricting to linear outcome models, and assuming that interference experienced by a unit does not depend on the unit's covariates. Our work addresses these shortcomings. We first provide and justify a novel definition of causal models with local interference. We prove that the True Average Causal Effect, a measure of causality where interference has been removed, can be identified in certain semi-parametric models satisfying this definition. These models allow for non-linearity, and also for interference to depend on a unit's covariates. An analytic estimand for the True Average Causal Effect is given in such settings. We further prove that the True Average Causal Effect cannot be identified in arbitrary models with local interference, showing that identification requires semi-parametric assumptions. Finally, we provide an empirical validation of our method on both simulated and real-world datasets.

Nature versus nurture in galaxy formation: the effect of environment on star formation with causal machine learning

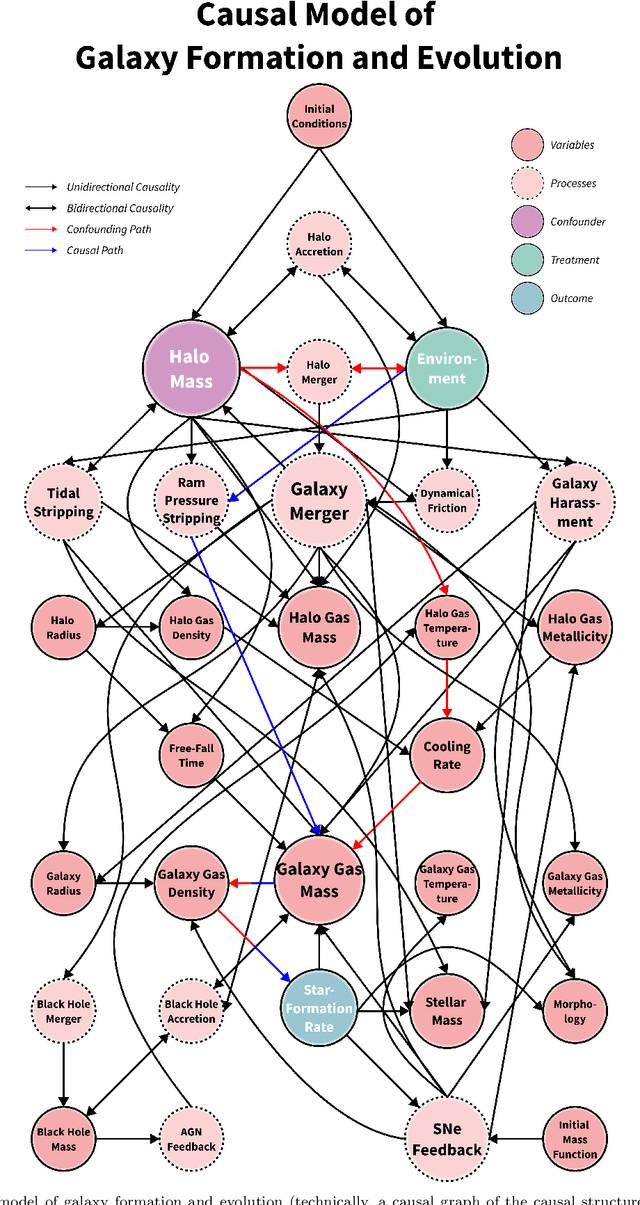
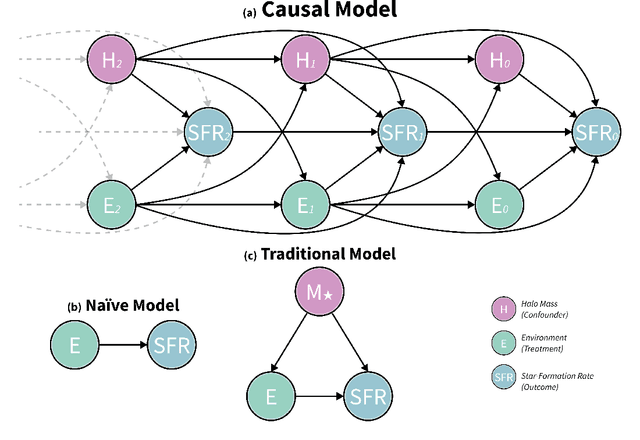
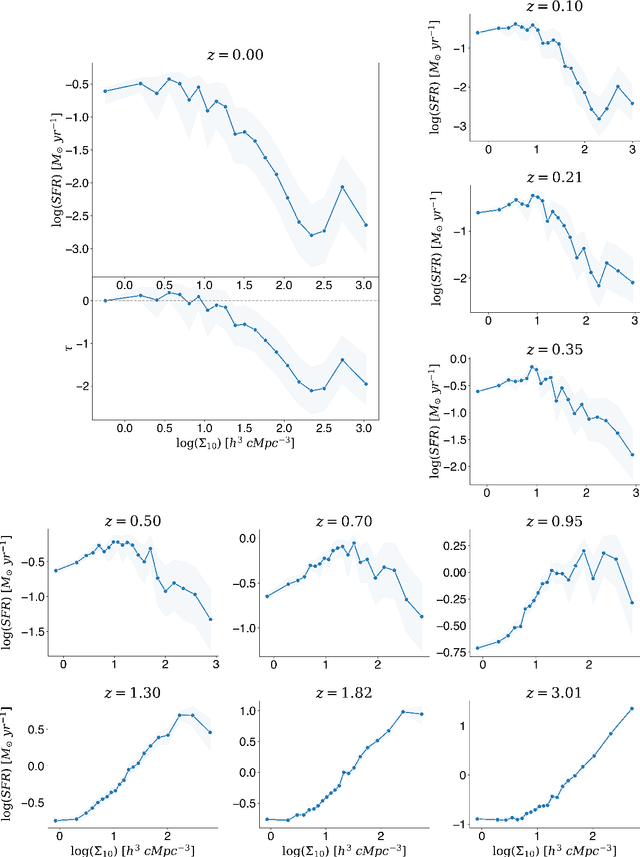
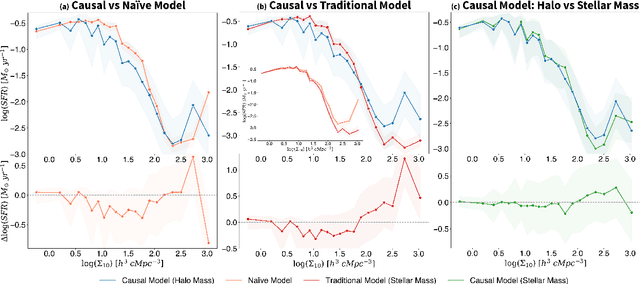
Understanding how galaxies form and evolve is at the heart of modern astronomy. With the advent of large-scale surveys and simulations, remarkable progress has been made in the last few decades. Despite this, the physical processes behind the phenomena, and particularly their importance, remain far from known, as correlations have primarily been established rather than the underlying causality. We address this challenge by applying the causal inference framework. Specifically, we tackle the fundamental open question of whether galaxy formation and evolution depends more on nature (i.e., internal processes) or nurture (i.e., external processes), by estimating the causal effect of environment on star-formation rate in the IllustrisTNG simulations. To do so, we develop a comprehensive causal model and employ cutting-edge techniques from epidemiology to overcome the long-standing problem of disentangling nature and nurture. We find that the causal effect is negative and substantial, with environment suppressing the SFR by a maximal factor of $\sim100$. While the overall effect at $z=0$ is negative, in the early universe, environment is discovered to have a positive impact, boosting star formation by a factor of $\sim10$ at $z\sim1$ and by even greater amounts at higher redshifts. Furthermore, we show that: (i) nature also plays an important role, as ignoring it underestimates the causal effect in intermediate-density environments by a factor of $\sim2$, (ii) controlling for the stellar mass at a snapshot in time, as is common in the literature, is not only insufficient to disentangle nature and nurture but actually has an adverse effect, though (iii) stellar mass is an adequate proxy of the effects of nature. Finally, this work may prove a useful blueprint for extracting causal insights in other fields that deal with dynamical systems with closed feedback loops, such as the Earth's climate.

Spillover Detection for Donor Selection in Synthetic Control Models

Synthetic control (SC) models are widely used to estimate causal effects in settings with observational time-series data. To identify the causal effect on a target unit, SC requires the existence of correlated units that are not impacted by the intervention. Given one of these potential donor units, how can we decide whether it is in fact a valid donor - that is, one not subject to spillover effects from the intervention? Such a decision typically requires appealing to strong a priori domain knowledge specifying the units, which becomes infeasible in situations with large pools of potential donors. In this paper, we introduce a practical, theoretically-grounded donor selection procedure, aiming to weaken this domain knowledge requirement. Our main result is a Theorem that yields the assumptions required to identify donor values at post-intervention time points using only pre-intervention data. We show how this Theorem - and the assumptions underpinning it - can be turned into a practical method for detecting potential spillover effects and excluding invalid donors when constructing SCs. Importantly, we employ sensitivity analysis to formally bound the bias in our SC causal estimate in situations where an excluded donor was indeed valid, or where a selected donor was invalid. Using ideas from the proximal causal inference and instrumental variables literature, we show that the excluded donors can nevertheless be leveraged to further debias causal effect estimates. Finally, we illustrate our donor selection procedure on both simulated and real-world datasets.

Disentangling Causal Effects from Sets of Interventions in the Presence of Unobserved Confounders

The ability to answer causal questions is crucial in many domains, as causal inference allows one to understand the impact of interventions. In many applications, only a single intervention is possible at a given time. However, in some important areas, multiple interventions are concurrently applied. Disentangling the effects of single interventions from jointly applied interventions is a challenging task -- especially as simultaneously applied interventions can interact. This problem is made harder still by unobserved confounders, which influence both treatments and outcome. We address this challenge by aiming to learn the effect of a single-intervention from both observational data and sets of interventions. We prove that this is not generally possible, but provide identification proofs demonstrating that it can be achieved under non-linear continuous structural causal models with additive, multivariate Gaussian noise -- even when unobserved confounders are present. Importantly, we show how to incorporate observed covariates and learn heterogeneous treatment effects. Based on the identifiability proofs, we provide an algorithm that learns the causal model parameters by pooling data from different regimes and jointly maximizing the combined likelihood. The effectiveness of our method is empirically demonstrated on both synthetic and real-world data.

Technology Readiness Levels for Machine Learning Systems

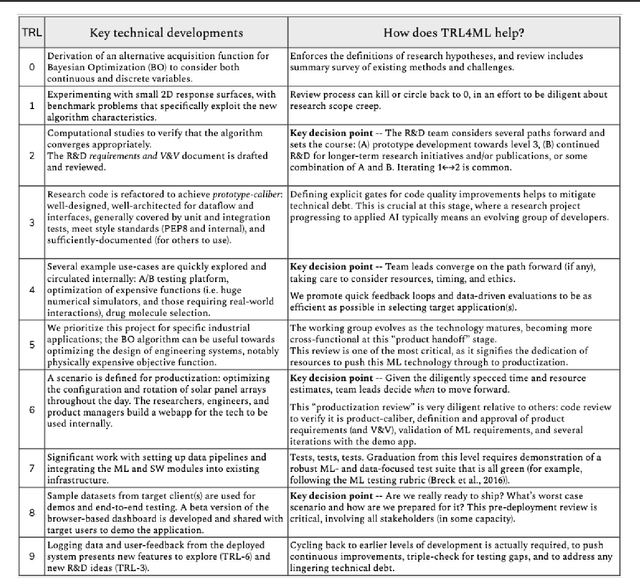
The development and deployment of machine learning (ML) systems can be executed easily with modern tools, but the process is typically rushed and means-to-an-end. The lack of diligence can lead to technical debt, scope creep and misaligned objectives, model misuse and failures, and expensive consequences. Engineering systems, on the other hand, follow well-defined processes and testing standards to streamline development for high-quality, reliable results. The extreme is spacecraft systems, where mission critical measures and robustness are ingrained in the development process. Drawing on experience in both spacecraft engineering and ML (from research through product across domain areas), we have developed a proven systems engineering approach for machine learning development and deployment. Our "Machine Learning Technology Readiness Levels" (MLTRL) framework defines a principled process to ensure robust, reliable, and responsible systems while being streamlined for ML workflows, including key distinctions from traditional software engineering. Even more, MLTRL defines a lingua franca for people across teams and organizations to work collaboratively on artificial intelligence and machine learning technologies. Here we describe the framework and elucidate it with several real world use-cases of developing ML methods from basic research through productization and deployment, in areas such as medical diagnostics, consumer computer vision, satellite imagery, and particle physics.