Christoph-Nikolas Straehle
Adaptive Bounding Box Uncertainties via Two-Step Conformal Prediction
Mar 12, 2024



Abstract:Quantifying a model's predictive uncertainty is essential for safety-critical applications such as autonomous driving. We consider quantifying such uncertainty for multi-object detection. In particular, we leverage conformal prediction to obtain uncertainty intervals with guaranteed coverage for object bounding boxes. One challenge in doing so is that bounding box predictions are conditioned on the object's class label. Thus, we develop a novel two-step conformal approach that propagates uncertainty in predicted class labels into the uncertainty intervals for the bounding boxes. This broadens the validity of our conformal coverage guarantees to include incorrectly classified objects, ensuring their usefulness when maximal safety assurances are required. Moreover, we investigate novel ensemble and quantile regression formulations to ensure the bounding box intervals are adaptive to object size, leading to a more balanced coverage across sizes. Validating our two-step approach on real-world datasets for 2D bounding box localization, we find that desired coverage levels are satisfied with actionably tight predictive uncertainty intervals.
A powerful rank-based correction to multiple testing under positive dependency
Nov 17, 2023Abstract:We develop a novel multiple hypothesis testing correction with family-wise error rate (FWER) control that efficiently exploits positive dependencies between potentially correlated statistical hypothesis tests. Our proposed algorithm $\texttt{max-rank}$ is conceptually straight-forward, relying on the use of a $\max$-operator in the rank domain of computed test statistics. We compare our approach to the frequently employed Bonferroni correction, theoretically and empirically demonstrating its superiority over Bonferroni in the case of existing positive dependency, and its equivalence otherwise. Our advantage over Bonferroni increases as the number of tests rises, and we maintain high statistical power whilst ensuring FWER control. We specifically frame our algorithm in the context of parallel permutation testing, a scenario that arises in our primary application of conformal prediction, a recently popularized approach for quantifying uncertainty in complex predictive settings.
Anomaly Detection using Contrastive Normalizing Flows
Aug 30, 2022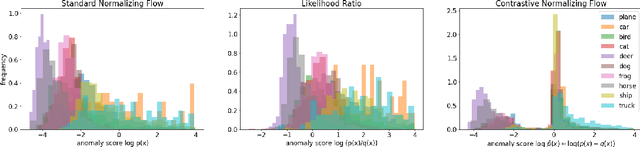
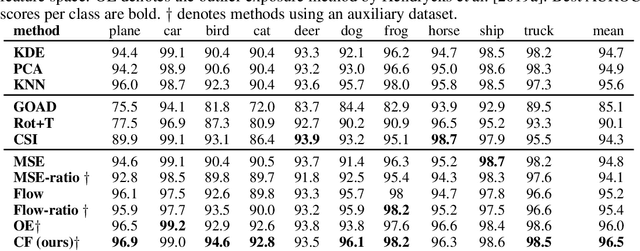


Abstract:Detecting test data deviating from training data is a central problem for safe and robust machine learning. Likelihoods learned by a generative model, e.g., a normalizing flow via standard log-likelihood training, perform poorly as an anomaly score. We propose to use an unlabelled auxiliary dataset and a probabilistic outlier score for anomaly detection. We use a self-supervised feature extractor trained on the auxiliary dataset and train a normalizing flow on the extracted features by maximizing the likelihood on in-distribution data and minimizing the likelihood on the auxiliary dataset. We show that this is equivalent to learning the normalized positive difference between the in-distribution and the auxiliary feature density. We conduct experiments on benchmark datasets and show a robust improvement compared to likelihood, likelihood ratio methods and state-of-the-art anomaly detection methods.
Fail-Safe Generative Adversarial Imitation Learning
Mar 03, 2022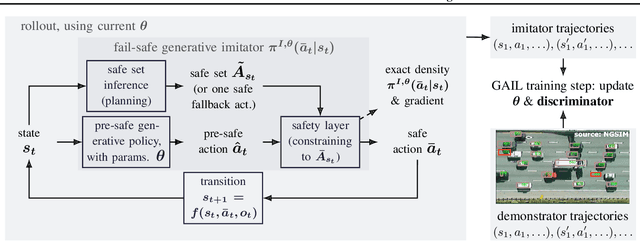


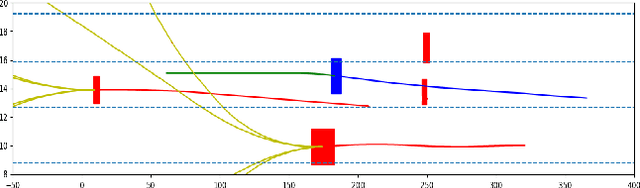
Abstract:For flexible yet safe imitation learning (IL), we propose a modular approach that uses a generative imitator policy with a safety layer, has an overall explicit density/gradient, can therefore be end-to-end trained using generative adversarial IL (GAIL), and comes with theoretical worst-case safety/robustness guarantees. The safety layer's exact density comes from using a countable non-injective gluing of piecewise differentiable injections and the change-of-variables formula. The safe set (into which the safety layer maps) is inferred by sampling actions and their potential future fail-safe fallback continuations, together with Lipschitz continuity and convexity arguments. We also provide theoretical bounds showing the advantage of using the safety layer already during training (imitation error linear in the horizon) compared to only using it at test time (quadratic error). In an experiment on challenging real-world driver interaction data, we empirically demonstrate tractability, safety and imitation performance of our approach.
Imitation Learning by State-Only Distribution Matching
Feb 09, 2022Abstract:Imitation Learning from observation describes policy learning in a similar way to human learning. An agent's policy is trained by observing an expert performing a task. While many state-only imitation learning approaches are based on adversarial imitation learning, one main drawback is that adversarial training is often unstable and lacks a reliable convergence estimator. If the true environment reward is unknown and cannot be used to select the best-performing model, this can result in bad real-world policy performance. We propose a non-adversarial learning-from-observations approach, together with an interpretable convergence and performance metric. Our training objective minimizes the Kulback-Leibler divergence (KLD) between the policy and expert state transition trajectories which can be optimized in a non-adversarial fashion. Such methods demonstrate improved robustness when learned density models guide the optimization. We further improve the sample efficiency by rewriting the KLD minimization as the Soft Actor Critic objective based on a modified reward using additional density models that estimate the environment's forward and backward dynamics. Finally, we evaluate the effectiveness of our approach on well-known continuous control environments and show state-of-the-art performance while having a reliable performance estimator compared to several recent learning-from-observation methods.
Haar Wavelet based Block Autoregressive Flows for Trajectories
Sep 21, 2020



Abstract:Prediction of trajectories such as that of pedestrians is crucial to the performance of autonomous agents. While previous works have leveraged conditional generative models like GANs and VAEs for learning the likely future trajectories, accurately modeling the dependency structure of these multimodal distributions, particularly over long time horizons remains challenging. Normalizing flow based generative models can model complex distributions admitting exact inference. These include variants with split coupling invertible transformations that are easier to parallelize compared to their autoregressive counterparts. To this end, we introduce a novel Haar wavelet based block autoregressive model leveraging split couplings, conditioned on coarse trajectories obtained from Haar wavelet based transformations at different levels of granularity. This yields an exact inference method that models trajectories at different spatio-temporal resolutions in a hierarchical manner. We illustrate the advantages of our approach for generating diverse and accurate trajectories on two real-world datasets - Stanford Drone and Intersection Drone.
Multiagent trajectory models via game theory and implicit layer-based learning
Sep 17, 2020

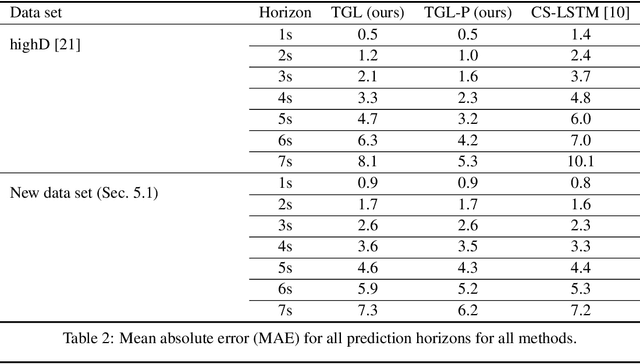

Abstract:For prediction of interacting agents' trajectories, we propose an end-to-end trainable architecture that hybridizes neural nets with game-theoretic reasoning, has interpretable intermediate representations, and transfers to robust downstream decision making. It combines (1) a differentiable implicit layer that maps preferences to local Nash equilibria with (2) a learned equilibrium refinement concept and (3) a learned preference revelation net, given initial trajectories as input. This is accompanied by a new class of continuous potential games. We provide theoretical results for explicit gradients and soundness, and several measures to ensure tractability. In experiments, we evaluate our approach on two real-world data sets, where we predict highway driver merging trajectories, and on a simple decision-making transfer task.
Non-cooperative Multi-agent Systems with Exploring Agents
May 25, 2020

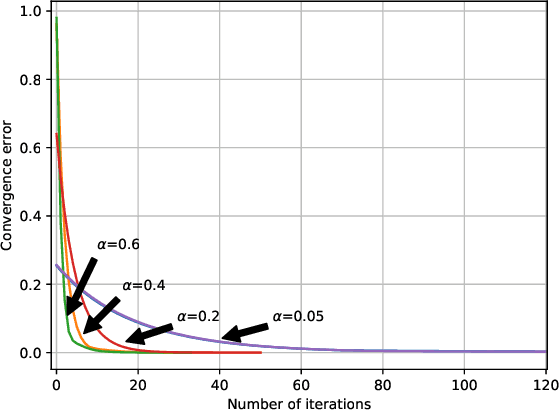

Abstract:Multi-agent learning is a challenging problem in machine learning that has applications in different domains such as distributed control, robotics, and economics. We develop a prescriptive model of multi-agent behavior using Markov games. Since in many multi-agent systems, agents do not necessary select their optimum strategies against other agents (e.g., multi-pedestrian interaction), we focus on models in which the agents play "exploration but near optimum strategies". We model such policies using the Boltzmann-Gibbs distribution. This leads to a set of coupled Bellman equations that describes the behavior of the agents. We introduce a set of conditions under which the set of equations admit a unique solution and propose two algorithms that provably provide the solution in finite and infinite time horizon scenarios. We also study a practical setting in which the interactions can be described using the occupancy measures and propose a simplified Markov game with less complexity. Furthermore, we establish the connection between the Markov games with exploration strategies and the principle of maximum causal entropy for multi-agent systems. Finally, we evaluate the performance of our algorithms via several well-known games from the literature and some games that are designed based on real world applications.
Conditional Flow Variational Autoencoders for Structured Sequence Prediction
Aug 24, 2019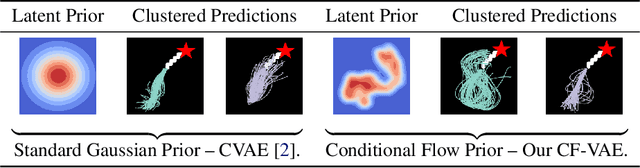



Abstract:Prediction of future states of the environment and interacting agents is a key competence required for autonomous agents to operate successfully in the real world. Prior work for structured sequence prediction based on latent variable models imposes a uni-modal standard Gaussian prior on the latent variables. This induces a strong model bias which makes it challenging to fully capture the multi-modality of the distribution of the future states. In this work, we introduce Conditional Flow Variational Autoencoders which uses our novel conditional normalizing flow based prior. We show that using our novel complex multi-modal conditional prior we can capture complex multi-modal conditional distributions. Furthermore, we study for the first time latent variable collapse with normalizing flows and propose solutions to prevent such failure cases. Our experiments on three multi-modal structured sequence prediction datasets -- MNIST Sequences, Stanford Drone and HighD -- show that the proposed method obtains state of art results across different evaluation metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge