Non-cooperative Multi-agent Systems with Exploring Agents
Paper and Code
May 25, 2020

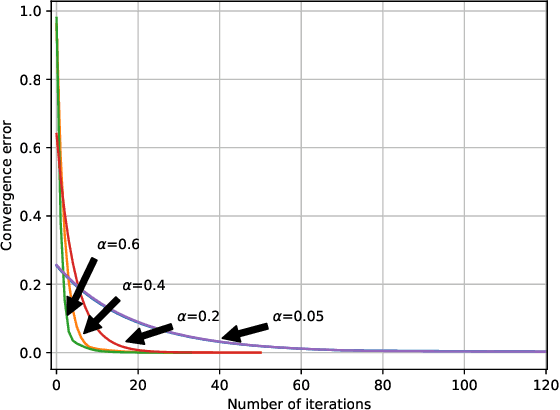

Multi-agent learning is a challenging problem in machine learning that has applications in different domains such as distributed control, robotics, and economics. We develop a prescriptive model of multi-agent behavior using Markov games. Since in many multi-agent systems, agents do not necessary select their optimum strategies against other agents (e.g., multi-pedestrian interaction), we focus on models in which the agents play "exploration but near optimum strategies". We model such policies using the Boltzmann-Gibbs distribution. This leads to a set of coupled Bellman equations that describes the behavior of the agents. We introduce a set of conditions under which the set of equations admit a unique solution and propose two algorithms that provably provide the solution in finite and infinite time horizon scenarios. We also study a practical setting in which the interactions can be described using the occupancy measures and propose a simplified Markov game with less complexity. Furthermore, we establish the connection between the Markov games with exploration strategies and the principle of maximum causal entropy for multi-agent systems. Finally, we evaluate the performance of our algorithms via several well-known games from the literature and some games that are designed based on real world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge