Multiagent trajectory models via game theory and implicit layer-based learning
Paper and Code
Sep 17, 2020

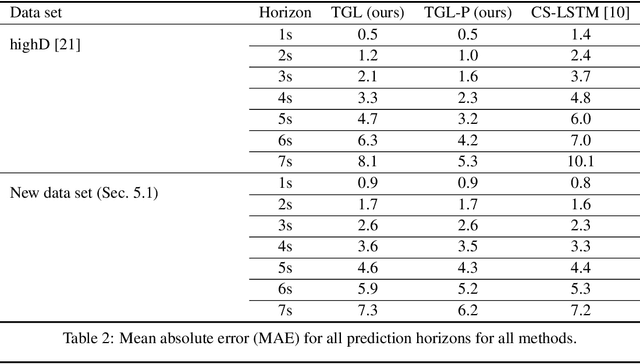

For prediction of interacting agents' trajectories, we propose an end-to-end trainable architecture that hybridizes neural nets with game-theoretic reasoning, has interpretable intermediate representations, and transfers to robust downstream decision making. It combines (1) a differentiable implicit layer that maps preferences to local Nash equilibria with (2) a learned equilibrium refinement concept and (3) a learned preference revelation net, given initial trajectories as input. This is accompanied by a new class of continuous potential games. We provide theoretical results for explicit gradients and soundness, and several measures to ensure tractability. In experiments, we evaluate our approach on two real-world data sets, where we predict highway driver merging trajectories, and on a simple decision-making transfer task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge