Fuzzy clustering of ordinal time series based on two novel distances with economic applications

Time series clustering is a central machine learning task with applications in many fields. While the majority of the methods focus on real-valued time series, very few works consider series with discrete response. In this paper, the problem of clustering ordinal time series is addressed. To this aim, two novel distances between ordinal time series are introduced and used to construct fuzzy clustering procedures. Both metrics are functions of the estimated cumulative probabilities, thus automatically taking advantage of the ordering inherent to the series' range. The resulting clustering algorithms are computationally efficient and able to group series generated from similar stochastic processes, reaching accurate results even though the series come from a wide variety of models. Since the dynamic of the series may vary over the time, we adopt a fuzzy approach, thus enabling the procedures to locate each series into several clusters with different membership degrees. An extensive simulation study shows that the proposed methods outperform several alternative procedures. Weighted versions of the clustering algorithms are also presented and their advantages with respect to the original methods are discussed. Two specific applications involving economic time series illustrate the usefulness of the proposed approaches.

Social navigation with human empowerment driven reinforcement learning

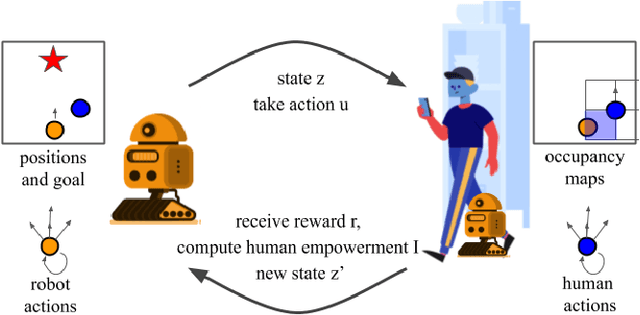
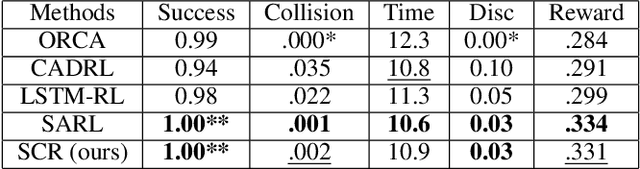
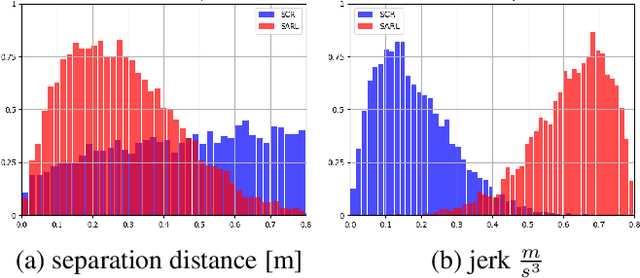
The next generation of mobile robots needs to be socially-compliant to be accepted by humans. As simple as this task may seem, defining compliance formally is not trivial. Yet, classical reinforcement learning (RL) relies upon hard-coded reward signals. In this work, we go beyond this approach and provide the agent with intrinsic motivation using empowerment. Empowerment maximizes the influence of an agent on its near future and has been shown to be a good model for biological behaviors. It also has been used for artificial agents to learn complicated and generalized actions. Self-empowerment maximizes the influence of an agent on its future. On the contrary, our robot strives for the empowerment of people in its environment, so they are not disturbed by the robot when pursuing their goals. We show that our robot has a positive influence on humans, as it minimizes the travel time and distance of humans while moving efficiently to its own goal. The method can be used in any multi-agent system that requires a robot to solve a particular task involving humans interactions.

SafeCritic: Collision-Aware Trajectory Prediction

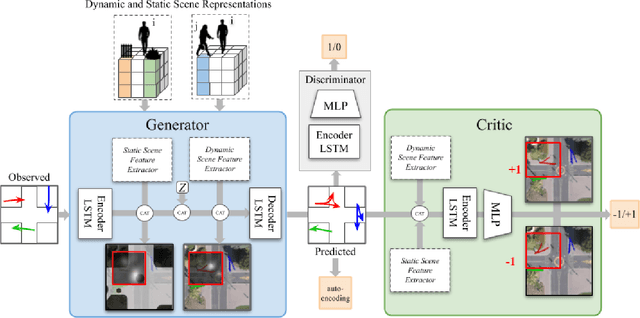
Navigating complex urban environments safely is a key to realize fully autonomous systems. Predicting future locations of vulnerable road users, such as pedestrians and cyclists, thus, has received a lot of attention in the recent years. While previous works have addressed modeling interactions with the static (obstacles) and dynamic (humans) environment agents, we address an important gap in trajectory prediction. We propose SafeCritic, a model that synergizes generative adversarial networks for generating multiple "real" trajectories with reinforcement learning to generate "safe" trajectories. The Discriminator evaluates the generated candidates on whether they are consistent with the observed inputs. The Critic network is environmentally aware to prune trajectories that are in collision or are in violation with the environment. The auto-encoding loss stabilizes training and prevents mode-collapse. We demonstrate results on two large scale data sets with a considerable improvement over state-of-the-art. We also show that the Critic is able to classify the safety of trajectories.

Dictionary Learning Strategies for Compressed Fiber Sensing Using a Probabilistic Sparse Model

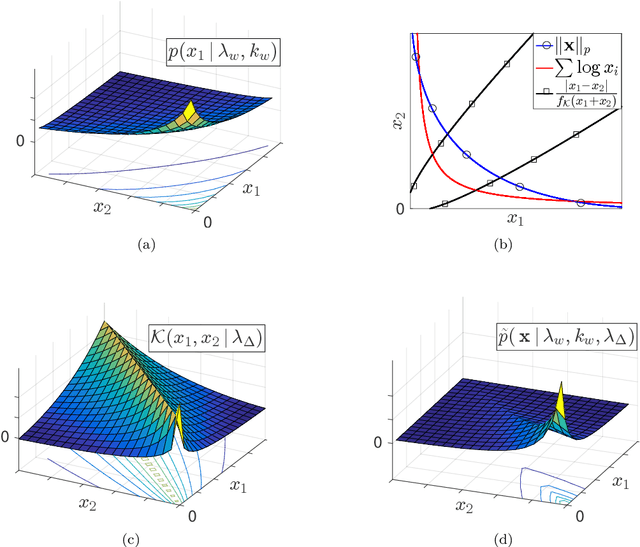
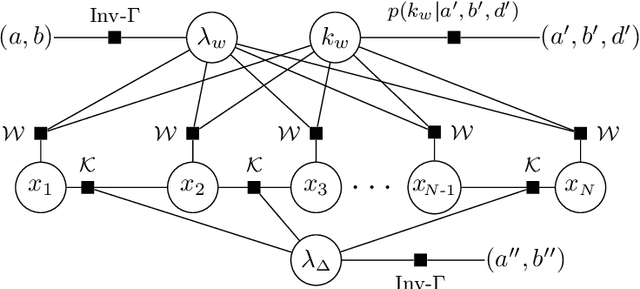
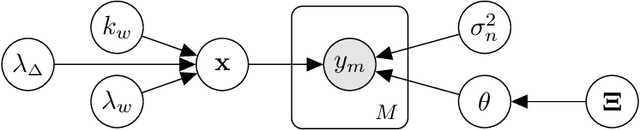
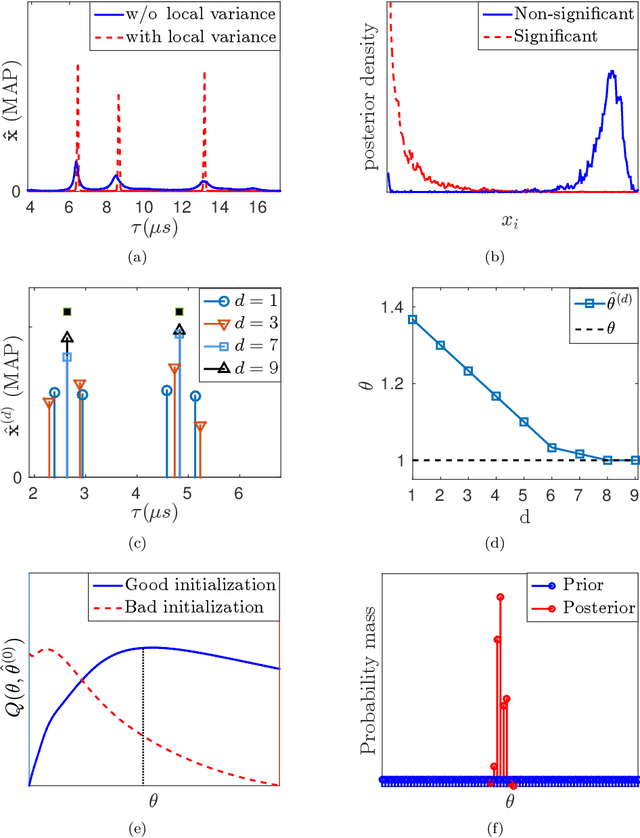
We present a sparse estimation and dictionary learning framework for compressed fiber sensing based on a probabilistic hierarchical sparse model. To handle severe dictionary coherence, selective shrinkage is achieved using a Weibull prior, which can be related to non-convex optimization with $p$-norm constraints for $0 < p < 1$. In addition, we leverage the specific dictionary structure to promote collective shrinkage based on a local similarity model. This is incorporated in form of a kernel function in the joint prior density of the sparse coefficients, thereby establishing a Markov random field-relation. Approximate inference is accomplished using a hybrid technique that combines Hamilton Monte Carlo and Gibbs sampling. To estimate the dictionary parameter, we pursue two strategies, relying on either a deterministic or a probabilistic model for the dictionary parameter. In the first strategy, the parameter is estimated based on alternating estimation. In the second strategy, it is jointly estimated along with the sparse coefficients. The performance is evaluated in comparison to an existing method in various scenarios using simulations and experimental data.