Dictionary Learning Strategies for Compressed Fiber Sensing Using a Probabilistic Sparse Model
Paper and Code
Oct 21, 2016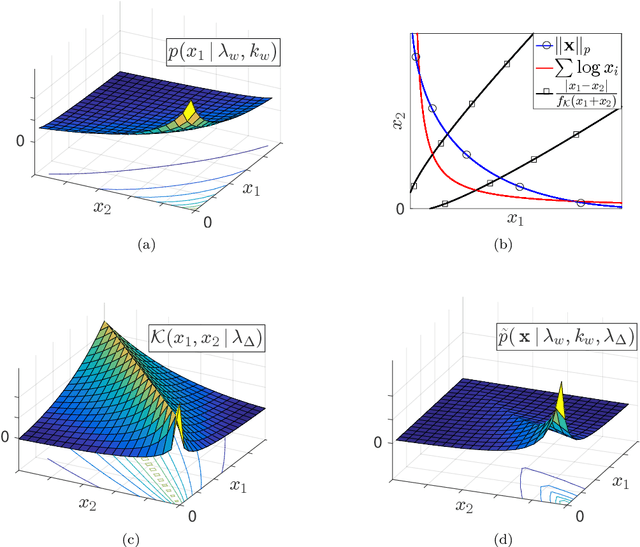
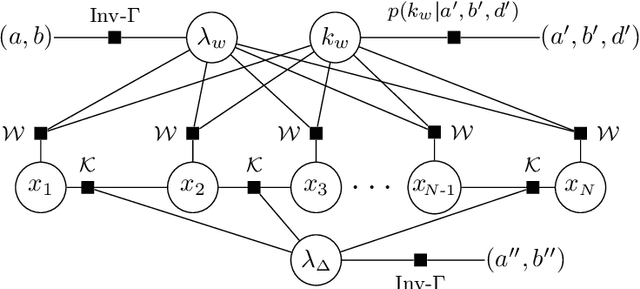
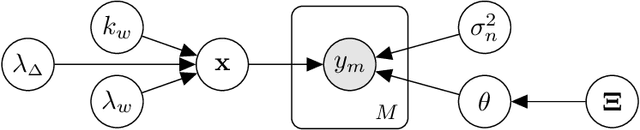
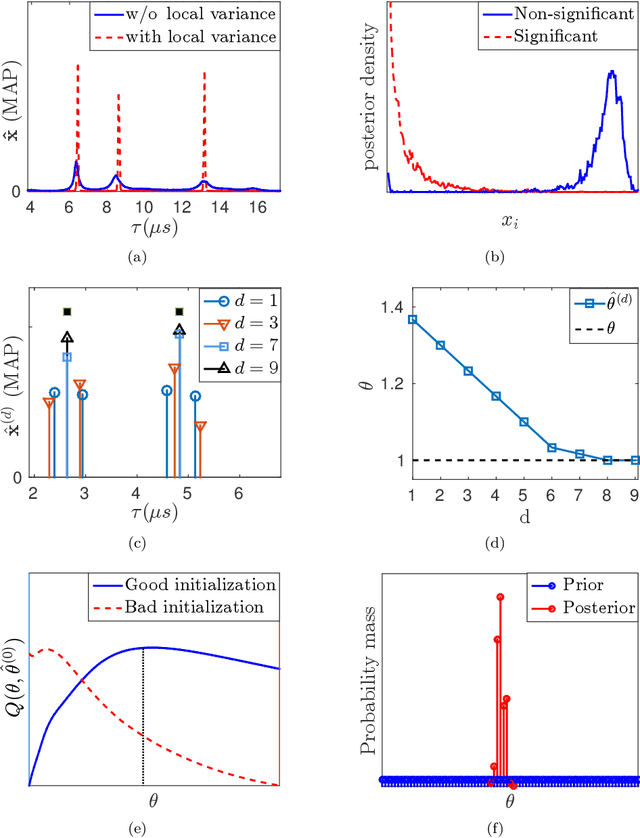
We present a sparse estimation and dictionary learning framework for compressed fiber sensing based on a probabilistic hierarchical sparse model. To handle severe dictionary coherence, selective shrinkage is achieved using a Weibull prior, which can be related to non-convex optimization with $p$-norm constraints for $0 < p < 1$. In addition, we leverage the specific dictionary structure to promote collective shrinkage based on a local similarity model. This is incorporated in form of a kernel function in the joint prior density of the sparse coefficients, thereby establishing a Markov random field-relation. Approximate inference is accomplished using a hybrid technique that combines Hamilton Monte Carlo and Gibbs sampling. To estimate the dictionary parameter, we pursue two strategies, relying on either a deterministic or a probabilistic model for the dictionary parameter. In the first strategy, the parameter is estimated based on alternating estimation. In the second strategy, it is jointly estimated along with the sparse coefficients. The performance is evaluated in comparison to an existing method in various scenarios using simulations and experimental data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge