Skywork R1V2: Multimodal Hybrid Reinforcement Learning for Reasoning

We present Skywork R1V2, a next-generation multimodal reasoning model and a major leap forward from its predecessor, Skywork R1V. At its core, R1V2 introduces a hybrid reinforcement learning paradigm that harmonizes reward-model guidance with rule-based strategies, thereby addressing the long-standing challenge of balancing sophisticated reasoning capabilities with broad generalization. To further enhance training efficiency, we propose the Selective Sample Buffer (SSB) mechanism, which effectively counters the ``Vanishing Advantages'' dilemma inherent in Group Relative Policy Optimization (GRPO) by prioritizing high-value samples throughout the optimization process. Notably, we observe that excessive reinforcement signals can induce visual hallucinations--a phenomenon we systematically monitor and mitigate through calibrated reward thresholds throughout the training process. Empirical results affirm the exceptional capability of R1V2, with benchmark-leading performances such as 62.6 on OlympiadBench, 79.0 on AIME2024, 63.6 on LiveCodeBench, and 74.0 on MMMU. These results underscore R1V2's superiority over existing open-source models and demonstrate significant progress in closing the performance gap with premier proprietary systems, including Gemini 2.5 and OpenAI o4-mini. The Skywork R1V2 model weights have been publicly released to promote openness and reproducibility https://huggingface.co/Skywork/Skywork-R1V2-38B.

Skywork R1V: Pioneering Multimodal Reasoning with Chain-of-Thought

We introduce Skywork R1V, a multimodal reasoning model extending the an R1-series Large language models (LLM) to visual modalities via an efficient multimodal transfer method. Leveraging a lightweight visual projector, Skywork R1V facilitates seamless multimodal adaptation without necessitating retraining of either the foundational language model or the vision encoder. To strengthen visual-text alignment, we propose a hybrid optimization strategy that combines Iterative Supervised Fine-Tuning (SFT) with Group Relative Policy Optimization (GRPO), significantly enhancing cross-modal integration efficiency. Additionally, we introduce an adaptive-length Chain-of-Thought distillation approach for reasoning data generation. This approach dynamically optimizes reasoning chain lengths, thereby enhancing inference efficiency and preventing excessive reasoning overthinking. Empirical evaluations demonstrate that Skywork R1V, with only 38B parameters, delivers competitive performance, achieving a score of 69.0 on the MMMU benchmark and 67.5 on MathVista. Meanwhile, it maintains robust textual reasoning performance, evidenced by impressive scores of 72.0 on AIME and 94.0 on MATH500. The Skywork R1V model weights have been publicly released to promote openness and reproducibility.

Stochastic Assignment for Deploying Multiple Marsupial Robots

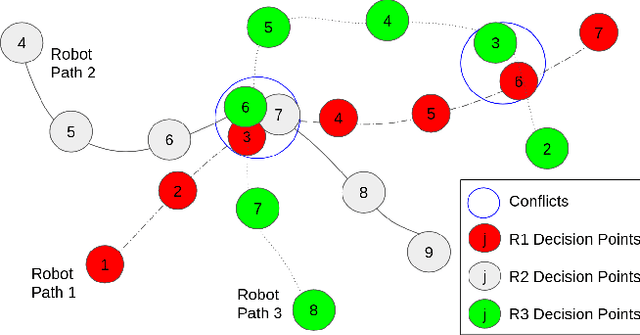
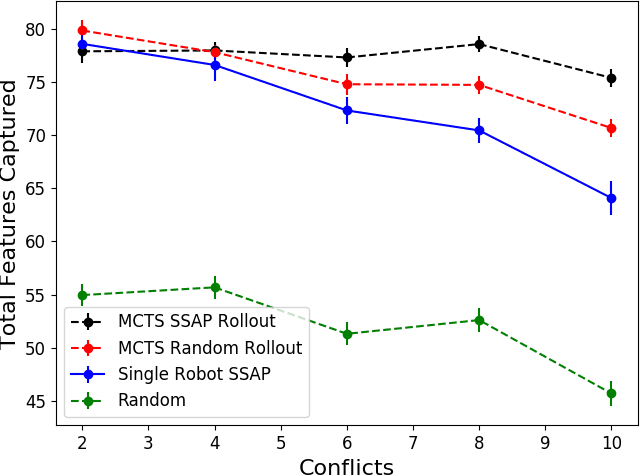
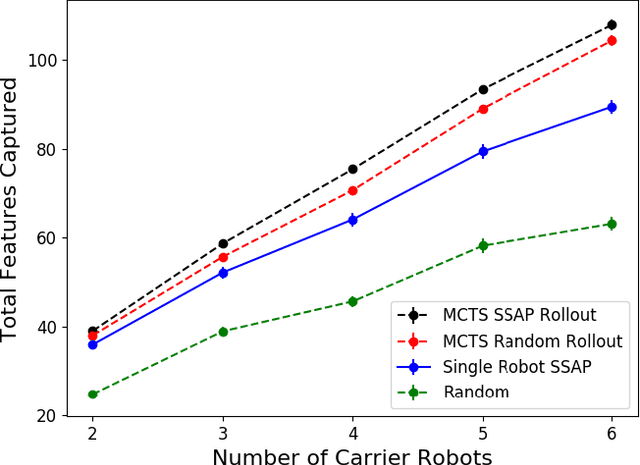
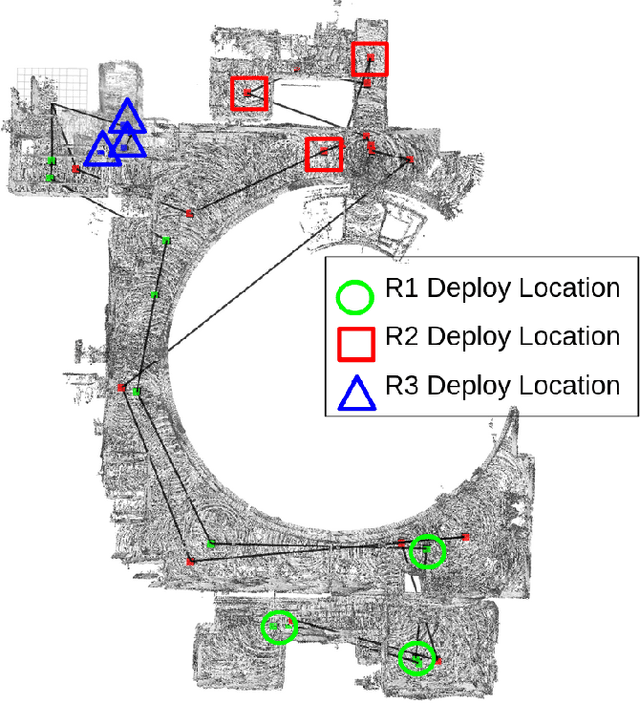
Marsupial robot teams consist of carrier robots that transport and deploy multiple passenger robots, such as a team of ground robots that carry and deploy multiple aerial robots, to rapidly explore complex environments. We specifically address the problem of planning the deployment times and locations of the carrier robots to best meet the objectives of a mission while reasoning over uncertain future observations and rewards. While prior work proposed optimal, polynomial-time solutions to single-carrier robot systems, the multiple-carrier robot deployment problem is fundamentally harder as it requires addressing conflicts and dependencies between deployments of multiple passenger robots. We propose a centralized heuristic search algorithm for the multiple-carrier robot deployment problem that combines Monte Carlo Tree Search with a dynamic programming-based solution to the Sequential Stochastic Assignment Problem as a rollout action-selection policy. Our results with both procedurally-generated data and data drawn from the DARPA Subterranean Challenge Urban Circuit show the viability of our approach and substantial exploration performance improvements over alternative algorithms.

Optimal Sequential Stochastic Deployment of Multiple Passenger Robots

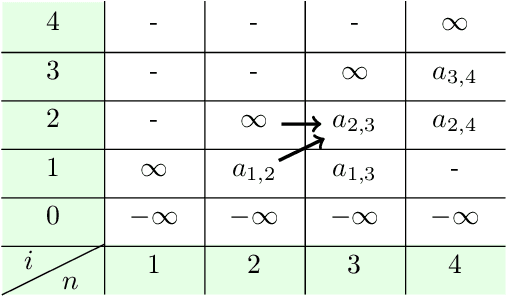
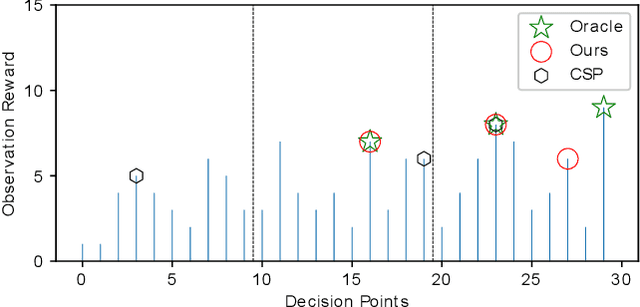
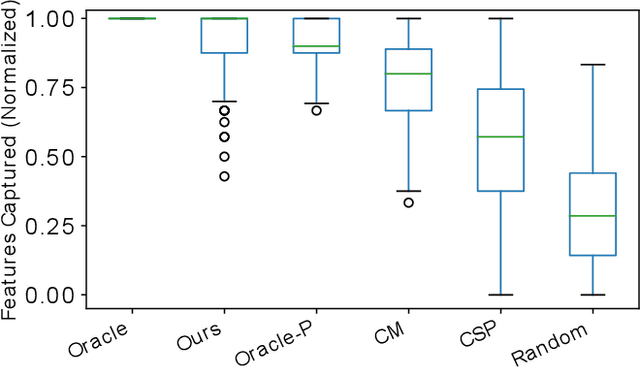
We present a new algorithm for deploying passenger robots in marsupial robot systems. A marsupial robot system consists of a carrier robot (e.g., a ground vehicle), which is highly capable and has a long mission duration, and at least one passenger robot (e.g., a short-duration aerial vehicle) transported by the carrier. We optimize the performance of passenger robot deployment by proposing an algorithm that reasons over uncertainty by exploiting information about the prior probability distribution of features of interest in the environment. Our algorithm is formulated as a solution to a sequential stochastic assignment problem (SSAP). The key feature of the algorithm is a recurrence relationship that defines a set of observation thresholds that are used to decide when to deploy passenger robots. Our algorithm computes the optimal policy in $O(NR)$ time, where $N$ is the number of deployment decision points and $R$ is the number of passenger robots to be deployed. We conducted drone deployment exploration experiments on real-world data from the DARPA Subterranean challenge to test the SSAP algorithm. Our results show that our deployment algorithm outperforms other competing algorithms, such as the classic secretary approach and baseline partitioning methods, and is comparable to an offline oracle algorithm.