Pareto GAN: Extending the Representational Power of GANs to Heavy-Tailed Distributions

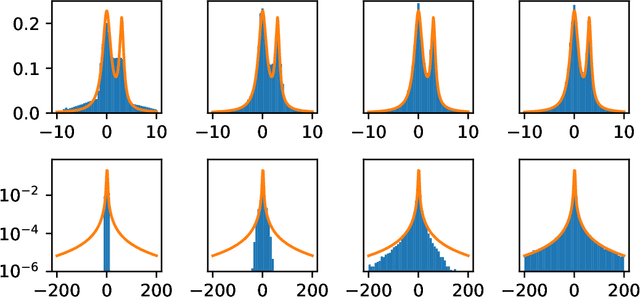
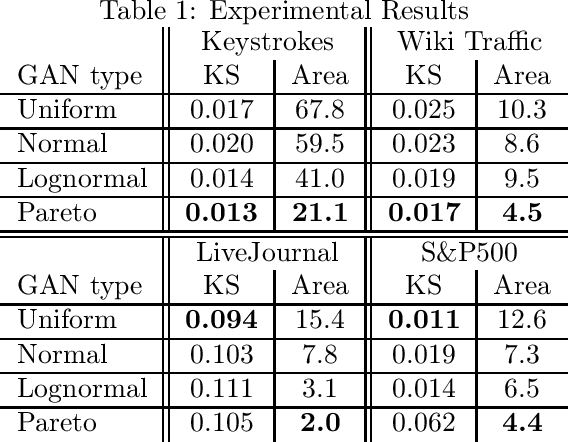
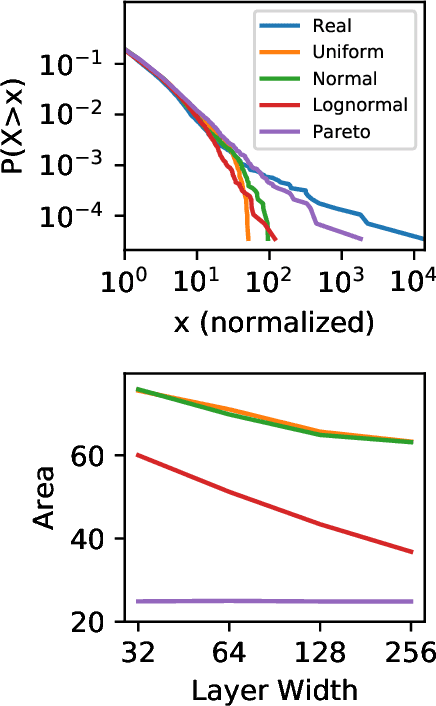
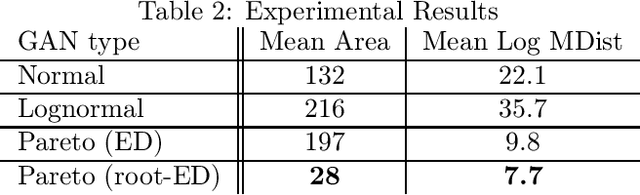
Generative adversarial networks (GANs) are often billed as "universal distribution learners", but precisely what distributions they can represent and learn is still an open question. Heavy-tailed distributions are prevalent in many different domains such as financial risk-assessment, physics, and epidemiology. We observe that existing GAN architectures do a poor job of matching the asymptotic behavior of heavy-tailed distributions, a problem that we show stems from their construction. Additionally, when faced with the infinite moments and large distances between outlier points that are characteristic of heavy-tailed distributions, common loss functions produce unstable or near-zero gradients. We address these problems with the Pareto GAN. A Pareto GAN leverages extreme value theory and the functional properties of neural networks to learn a distribution that matches the asymptotic behavior of the marginal distributions of the features. We identify issues with standard loss functions and propose the use of alternative metric spaces that enable stable and efficient learning. Finally, we evaluate our proposed approach on a variety of heavy-tailed datasets.

Limitations of the Lipschitz constant as a defense against adversarial examples

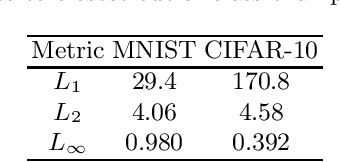
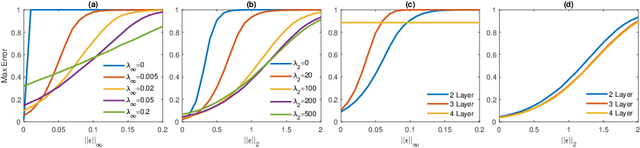
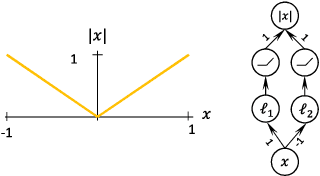
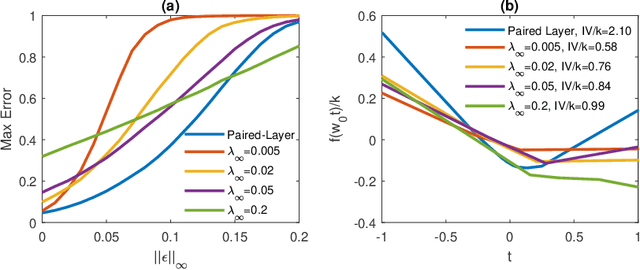
Several recent papers have discussed utilizing Lipschitz constants to limit the susceptibility of neural networks to adversarial examples. We analyze recently proposed methods for computing the Lipschitz constant. We show that the Lipschitz constant may indeed enable adversarially robust neural networks. However, the methods currently employed for computing it suffer from theoretical and practical limitations. We argue that addressing this shortcoming is a promising direction for future research into certified adversarial defenses.