Pareto GAN: Extending the Representational Power of GANs to Heavy-Tailed Distributions

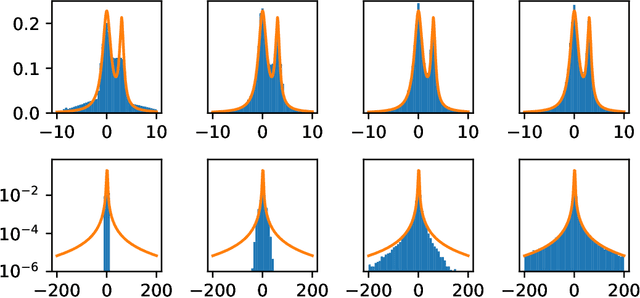
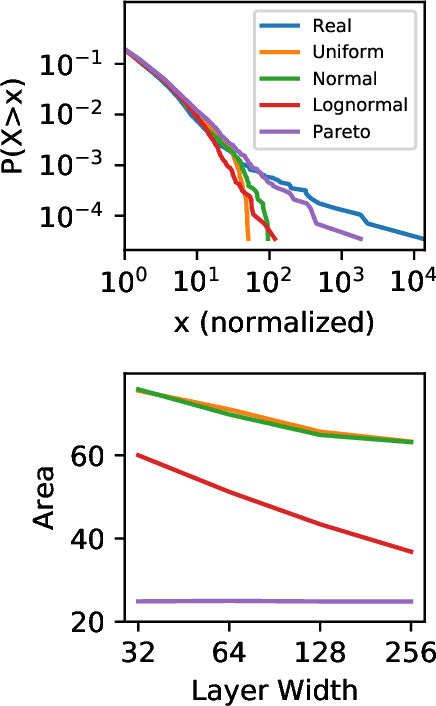
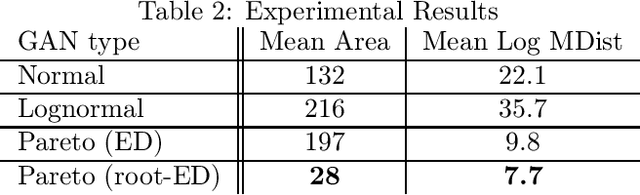
Generative adversarial networks (GANs) are often billed as "universal distribution learners", but precisely what distributions they can represent and learn is still an open question. Heavy-tailed distributions are prevalent in many different domains such as financial risk-assessment, physics, and epidemiology. We observe that existing GAN architectures do a poor job of matching the asymptotic behavior of heavy-tailed distributions, a problem that we show stems from their construction. Additionally, when faced with the infinite moments and large distances between outlier points that are characteristic of heavy-tailed distributions, common loss functions produce unstable or near-zero gradients. We address these problems with the Pareto GAN. A Pareto GAN leverages extreme value theory and the functional properties of neural networks to learn a distribution that matches the asymptotic behavior of the marginal distributions of the features. We identify issues with standard loss functions and propose the use of alternative metric spaces that enable stable and efficient learning. Finally, we evaluate our proposed approach on a variety of heavy-tailed datasets.

Universal Lipschitz Approximation in Bounded Depth Neural Networks

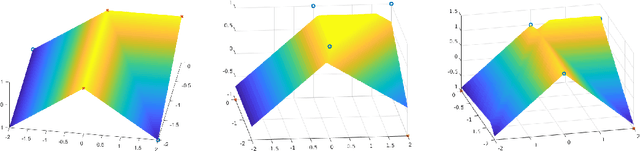
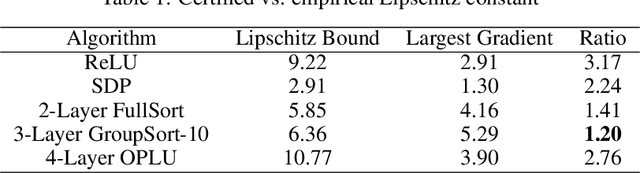
Adversarial attacks against machine learning models are a rather hefty obstacle to our increasing reliance on these models. Due to this, provably robust (certified) machine learning models are a major topic of interest. Lipschitz continuous models present a promising approach to solving this problem. By leveraging the expressive power of a variant of neural networks which maintain low Lipschitz constants, we prove that three layer neural networks using the FullSort activation function are Universal Lipschitz function Approximators (ULAs). This both explains experimental results and paves the way for the creation of better certified models going forward. We conclude by presenting experimental results that suggest that ULAs are a not just a novelty, but a competitive approach to providing certified classifiers, using these results to motivate several potential topics of further research.