Dual Alignment Maximin Optimization for Offline Model-based RL

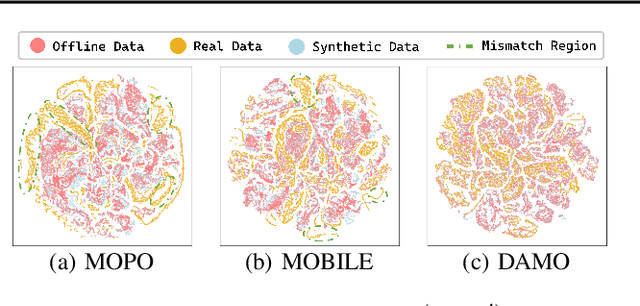
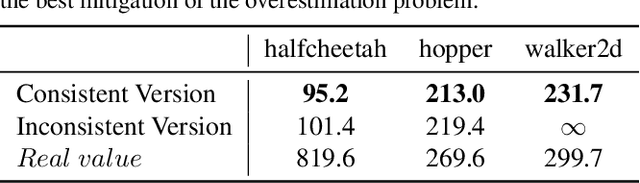
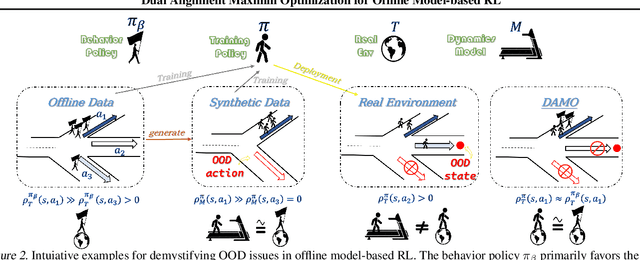
Offline reinforcement learning agents face significant deployment challenges due to the synthetic-to-real distribution mismatch. While most prior research has focused on improving the fidelity of synthetic sampling and incorporating off-policy mechanisms, the directly integrated paradigm often fails to ensure consistent policy behavior in biased models and underlying environmental dynamics, which inherently arise from discrepancies between behavior and learning policies. In this paper, we first shift the focus from model reliability to policy discrepancies while optimizing for expected returns, and then self-consistently incorporate synthetic data, deriving a novel actor-critic paradigm, Dual Alignment Maximin Optimization (DAMO). It is a unified framework to ensure both model-environment policy consistency and synthetic and offline data compatibility. The inner minimization performs dual conservative value estimation, aligning policies and trajectories to avoid out-of-distribution states and actions, while the outer maximization ensures that policy improvements remain consistent with inner value estimates. Empirical evaluations demonstrate that DAMO effectively ensures model and policy alignments, achieving competitive performance across diverse benchmark tasks.

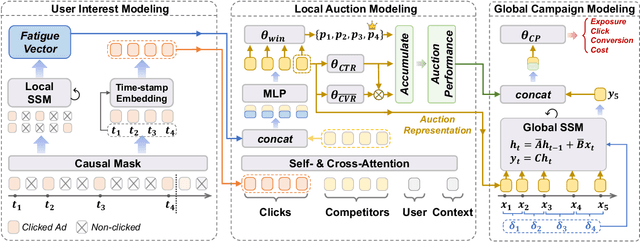
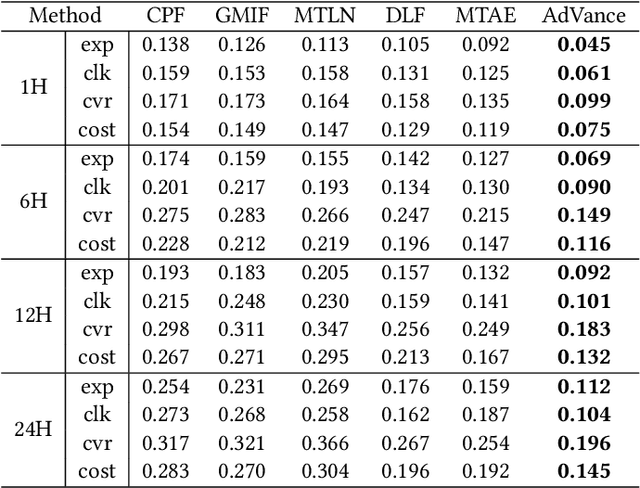
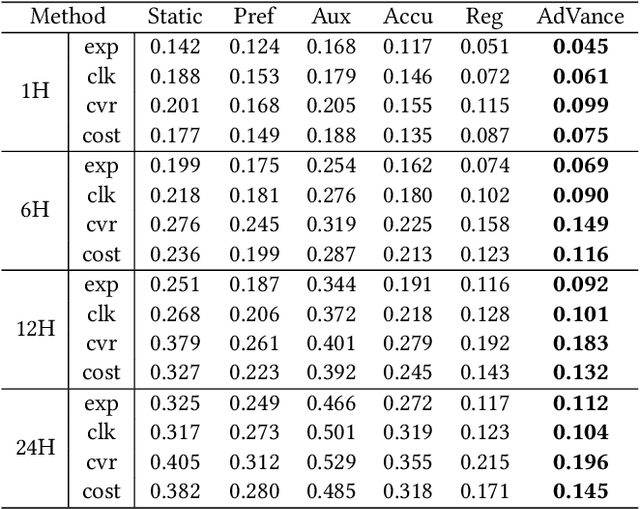
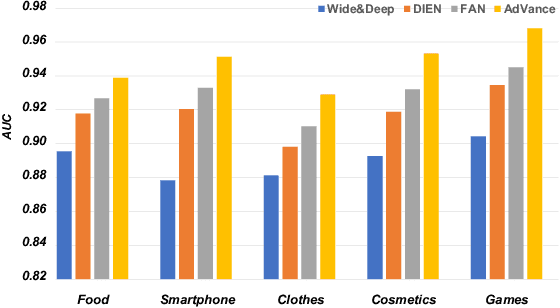
Know in AdVance: Linear-Complexity Forecasting of Ad Campaign Performance with Evolving User Interest

Real-time Bidding (RTB) advertisers wish to \textit{know in advance} the expected cost and yield of ad campaigns to avoid trial-and-error expenses. However, Campaign Performance Forecasting (CPF), a sequence modeling task involving tens of thousands of ad auctions, poses challenges of evolving user interest, auction representation, and long context, making coarse-grained and static-modeling methods sub-optimal. We propose \textit{AdVance}, a time-aware framework that integrates local auction-level and global campaign-level modeling. User preference and fatigue are disentangled using a time-positioned sequence of clicked items and a concise vector of all displayed items. Cross-attention, conditioned on the fatigue vector, captures the dynamics of user interest toward each candidate ad. Bidders compete with each other, presenting a complete graph similar to the self-attention mechanism. Hence, we employ a Transformer Encoder to compress each auction into embedding by solving auxiliary tasks. These sequential embeddings are then summarized by a conditional state space model (SSM) to comprehend long-range dependencies while maintaining global linear complexity. Considering the irregular time intervals between auctions, we make SSM's parameters dependent on the current auction embedding and the time interval. We further condition SSM's global predictions on the accumulation of local results. Extensive evaluations and ablation studies demonstrate its superiority over state-of-the-art methods. AdVance has been deployed on the Tencent Advertising platform, and A/B tests show a remarkable 4.5\% uplift in Average Revenue per User (ARPU).

Persistence B-Spline Grids: Stable Vector Representation of Persistence Diagrams Based on Data Fitting

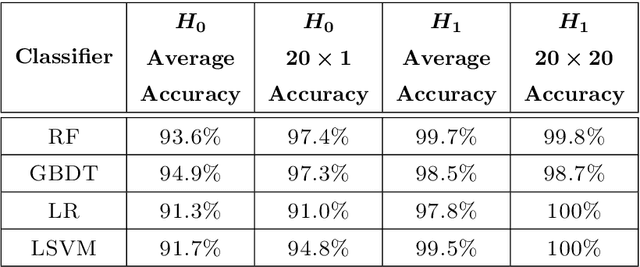
Over the last decades, many attempts have been made to optimally integrate machine learning (ML) and topological data analysis. A prominent problem in applying persistent homology to ML tasks is finding a vector representation of a persistence diagram (PD), which is a summary diagram for representing topological features. From the perspective of data fitting, a stable vector representation, persistence B-spline grid (PB), is proposed based on the efficient technique of progressive-iterative approximation for least-squares B-spline surface fitting. Meanwhile, we theoretically prove that the PB method is stable with respect to the metrics defined on the PD space, i.e., the $p$-Wasserstein distance and the bottleneck distance. The proposed method was tested on a synthetic dataset, datasets of randomly generated PDs, data of a dynamical system, and 3D CAD models.