Functional Network: A Novel Framework for Interpretability of Deep Neural Networks

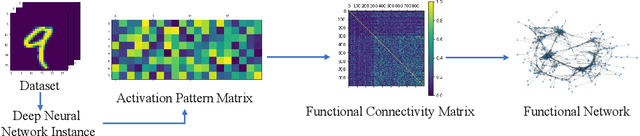
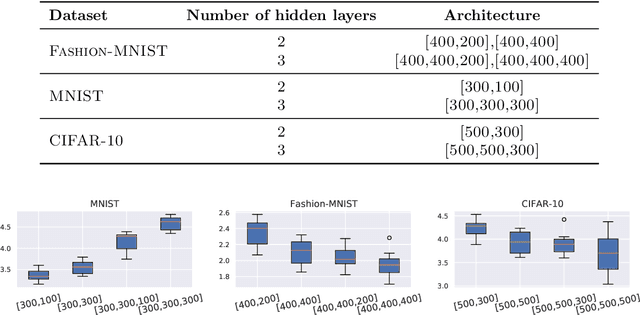
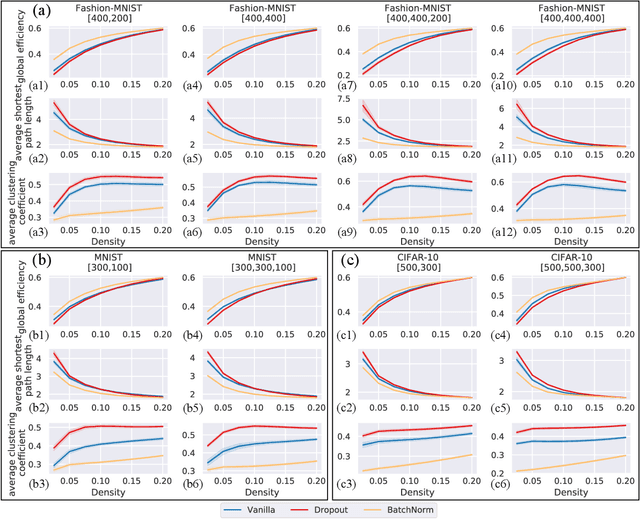
The layered structure of deep neural networks hinders the use of numerous analysis tools and thus the development of its interpretability. Inspired by the success of functional brain networks, we propose a novel framework for interpretability of deep neural networks, that is, the functional network. We construct the functional network of fully connected networks and explore its small-worldness. In our experiments, the mechanisms of regularization methods, namely, batch normalization and dropout, are revealed using graph theoretical analysis and topological data analysis. Our empirical analysis shows the following: (1) Batch normalization enhances model performance by increasing the global e ciency and the number of loops but reduces adversarial robustness by lowering the fault tolerance. (2) Dropout improves generalization and robustness of models by improving the functional specialization and fault tolerance. (3) The models with dierent regularizations can be clustered correctly according to their functional topological dierences, re ecting the great potential of the functional network and topological data analysis in interpretability.

Persistence B-Spline Grids: Stable Vector Representation of Persistence Diagrams Based on Data Fitting

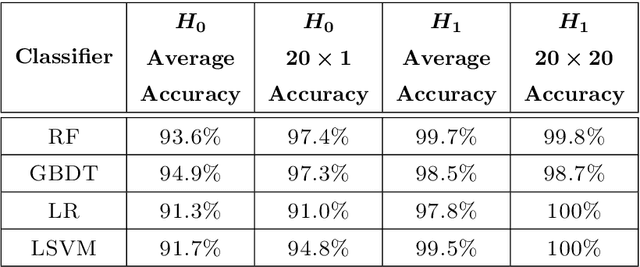
Over the last decades, many attempts have been made to optimally integrate machine learning (ML) and topological data analysis. A prominent problem in applying persistent homology to ML tasks is finding a vector representation of a persistence diagram (PD), which is a summary diagram for representing topological features. From the perspective of data fitting, a stable vector representation, persistence B-spline grid (PB), is proposed based on the efficient technique of progressive-iterative approximation for least-squares B-spline surface fitting. Meanwhile, we theoretically prove that the PB method is stable with respect to the metrics defined on the PD space, i.e., the $p$-Wasserstein distance and the bottleneck distance. The proposed method was tested on a synthetic dataset, datasets of randomly generated PDs, data of a dynamical system, and 3D CAD models.