Persistence B-Spline Grids: Stable Vector Representation of Persistence Diagrams Based on Data Fitting
Paper and Code
Sep 17, 2019
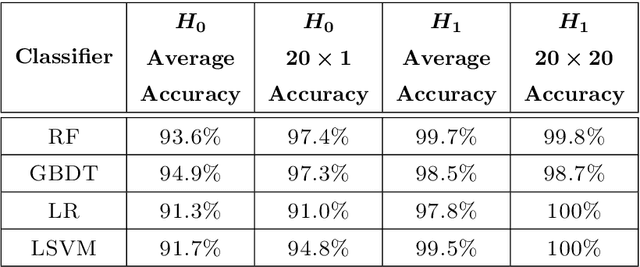

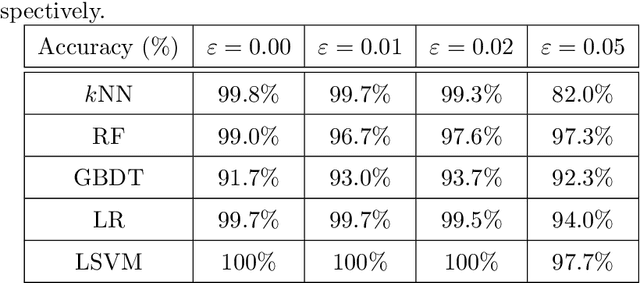
Over the last decades, many attempts have been made to optimally integrate machine learning (ML) and topological data analysis. A prominent problem in applying persistent homology to ML tasks is finding a vector representation of a persistence diagram (PD), which is a summary diagram for representing topological features. From the perspective of data fitting, a stable vector representation, persistence B-spline grid (PB), is proposed based on the efficient technique of progressive-iterative approximation for least-squares B-spline surface fitting. Meanwhile, we theoretically prove that the PB method is stable with respect to the metrics defined on the PD space, i.e., the $p$-Wasserstein distance and the bottleneck distance. The proposed method was tested on a synthetic dataset, datasets of randomly generated PDs, data of a dynamical system, and 3D CAD models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge