Predict and Resist: Long-Term Accident Anticipation under Sensor Noise

Accident anticipation is essential for proactive and safe autonomous driving, where even a brief advance warning can enable critical evasive actions. However, two key challenges hinder real-world deployment: (1) noisy or degraded sensory inputs from weather, motion blur, or hardware limitations, and (2) the need to issue timely yet reliable predictions that balance early alerts with false-alarm suppression. We propose a unified framework that integrates diffusion-based denoising with a time-aware actor-critic model to address these challenges. The diffusion module reconstructs noise-resilient image and object features through iterative refinement, preserving critical motion and interaction cues under sensor degradation. In parallel, the actor-critic architecture leverages long-horizon temporal reasoning and time-weighted rewards to determine the optimal moment to raise an alert, aligning early detection with reliability. Experiments on three benchmark datasets (DAD, CCD, A3D) demonstrate state-of-the-art accuracy and significant gains in mean time-to-accident, while maintaining robust performance under Gaussian and impulse noise. Qualitative analyses further show that our model produces earlier, more stable, and human-aligned predictions in both routine and highly complex traffic scenarios, highlighting its potential for real-world, safety-critical deployment.

VTutor: An Open-Source SDK for Generative AI-Powered Animated Pedagogical Agents with Multi-Media Output

The rapid evolution of large language models (LLMs) has transformed human-computer interaction (HCI), but the interaction with LLMs is currently mainly focused on text-based interactions, while other multi-model approaches remain under-explored. This paper introduces VTutor, an open-source Software Development Kit (SDK) that combines generative AI with advanced animation technologies to create engaging, adaptable, and realistic APAs for human-AI multi-media interactions. VTutor leverages LLMs for real-time personalized feedback, advanced lip synchronization for natural speech alignment, and WebGL rendering for seamless web integration. Supporting various 2D and 3D character models, VTutor enables researchers and developers to design emotionally resonant, contextually adaptive learning agents. This toolkit enhances learner engagement, feedback receptivity, and human-AI interaction while promoting trustworthy AI principles in education. VTutor sets a new standard for next-generation APAs, offering an accessible, scalable solution for fostering meaningful and immersive human-AI interaction experiences. The VTutor project is open-sourced and welcomes community-driven contributions and showcases.

PosFormer: Recognizing Complex Handwritten Mathematical Expression with Position Forest Transformer

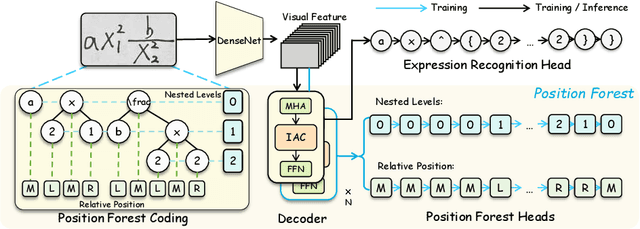
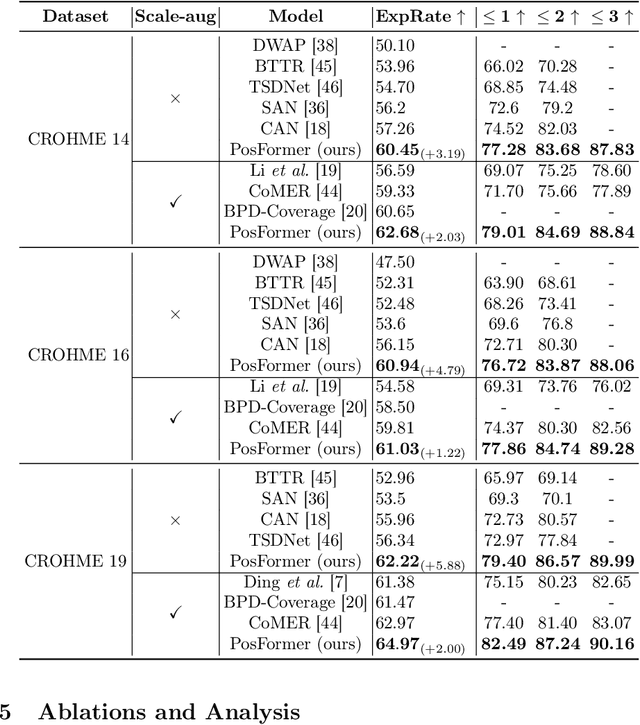
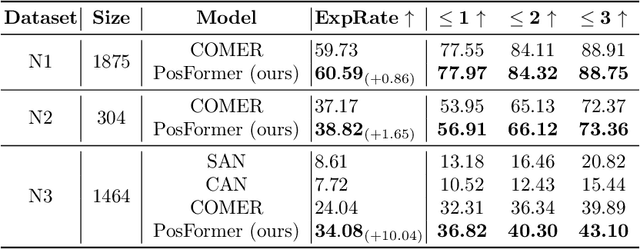
Handwritten Mathematical Expression Recognition (HMER) has wide applications in human-machine interaction scenarios, such as digitized education and automated offices. Recently, sequence-based models with encoder-decoder architectures have been commonly adopted to address this task by directly predicting LaTeX sequences of expression images. However, these methods only implicitly learn the syntax rules provided by LaTeX, which may fail to describe the position and hierarchical relationship between symbols due to complex structural relations and diverse handwriting styles. To overcome this challenge, we propose a position forest transformer (PosFormer) for HMER, which jointly optimizes two tasks: expression recognition and position recognition, to explicitly enable position-aware symbol feature representation learning. Specifically, we first design a position forest that models the mathematical expression as a forest structure and parses the relative position relationships between symbols. Without requiring extra annotations, each symbol is assigned a position identifier in the forest to denote its relative spatial position. Second, we propose an implicit attention correction module to accurately capture attention for HMER in the sequence-based decoder architecture. Extensive experiments validate the superiority of PosFormer, which consistently outperforms the state-of-the-art methods 2.03%/1.22%/2.00%, 1.83%, and 4.62% gains on the single-line CROHME 2014/2016/2019, multi-line M2E, and complex MNE datasets, respectively, with no additional latency or computational cost. Code is available at https://github.com/SJTU-DeepVisionLab/PosFormer.

New Distinguishers for Negation-Limited Weak Pseudorandom Functions

We show how to distinguish circuits with $\log k$ negations (a.k.a $k$-monotone functions) from uniformly random functions in $\exp\left(\tilde{O}\left(n^{1/3}k^{2/3}\right)\right)$ time using random samples. The previous best distinguisher, due to the learning algorithm by Blais, Cannone, Oliveira, Servedio, and Tan (RANDOM'15), requires $\exp\big(\tilde{O}(n^{1/2} k)\big)$ time. Our distinguishers are based on Fourier analysis on \emph{slices of the Boolean cube}. We show that some "middle" slices of negation-limited circuits have strong low-degree Fourier concentration and then we apply a variation of the classic Linial, Mansour, and Nisan "Low-Degree algorithm" (JACM'93) on slices. Our techniques also lead to a slightly improved weak learner for negation limited circuits under the uniform distribution.

Subspace Embedding and Linear Regression with Orlicz Norm

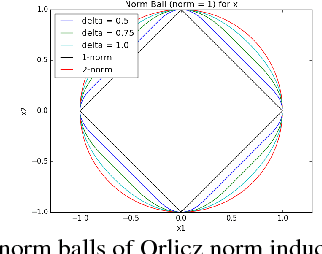
We consider a generalization of the classic linear regression problem to the case when the loss is an Orlicz norm. An Orlicz norm is parameterized by a non-negative convex function $G:\mathbb{R}_+\rightarrow\mathbb{R}_+$ with $G(0)=0$: the Orlicz norm of a vector $x\in\mathbb{R}^n$ is defined as $ \|x\|_G=\inf\left\{\alpha>0\large\mid\sum_{i=1}^n G(|x_i|/\alpha)\leq 1\right\}. $ We consider the cases where the function $G(\cdot)$ grows subquadratically. Our main result is based on a new oblivious embedding which embeds the column space of a given matrix $A\in\mathbb{R}^{n\times d}$ with Orlicz norm into a lower dimensional space with $\ell_2$ norm. Specifically, we show how to efficiently find an embedding matrix $S\in\mathbb{R}^{m\times n},m<n$ such that $\forall x\in\mathbb{R}^{d},\Omega(1/(d\log n)) \cdot \|Ax\|_G\leq \|SAx\|_2\leq O(d^2\log n) \cdot \|Ax\|_G.$ By applying this subspace embedding technique, we show an approximation algorithm for the regression problem $\min_{x\in\mathbb{R}^d} \|Ax-b\|_G$, up to a $O(d\log^2 n)$ factor. As a further application of our techniques, we show how to also use them to improve on the algorithm for the $\ell_p$ low rank matrix approximation problem for $1\leq p<2$.