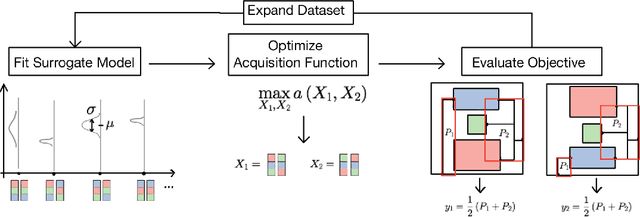
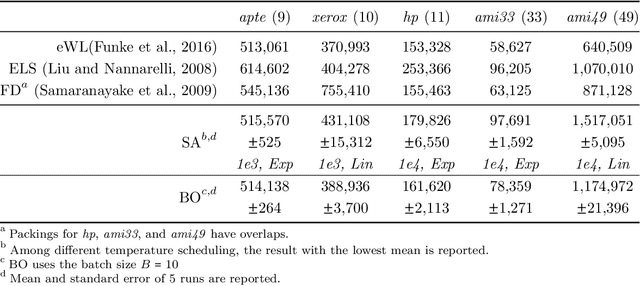
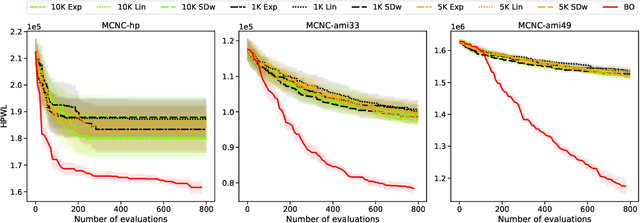
Bayesian Optimization for Macro Placement

Macro placement is the problem of placing memory blocks on a chip canvas. It can be formulated as a combinatorial optimization problem over sequence pairs, a representation which describes the relative positions of macros. Solving this problem is particularly challenging since the objective function is expensive to evaluate. In this paper, we develop a novel approach to macro placement using Bayesian optimization (BO) over sequence pairs. BO is a machine learning technique that uses a probabilistic surrogate model and an acquisition function that balances exploration and exploitation to efficiently optimize a black-box objective function. BO is more sample-efficient than reinforcement learning and therefore can be used with more realistic objectives. Additionally, the ability to learn from data and adapt the algorithm to the objective function makes BO an appealing alternative to other black-box optimization methods such as simulated annealing, which relies on problem-dependent heuristics and parameter-tuning. We benchmark our algorithm on the fixed-outline macro placement problem with the half-perimeter wire length objective and demonstrate competitive performance.

Batch Bayesian Optimization on Permutations using Acquisition Weighted Kernels

In this work we propose a batch Bayesian optimization method for combinatorial problems on permutations, which is well suited for expensive cost functions on permutations. We introduce LAW, a new efficient batch acquisition method based on the determinantal point process, using an acquisition weighted kernel. Relying on multiple parallel evaluations, LAW accelerates the search for the optimal permutation. We provide a regret analysis for our method to gain insight in its theoretical properties. We then apply the framework to permutation problems, which have so far received little attention in the Bayesian Optimization literature, despite their practical importance. We call this method LAW2ORDER. We evaluate the method on several standard combinatorial problems involving permutations such as quadratic assignment, flowshop scheduling and the traveling salesman, as well as on a structure learning task.

Mixed Variable Bayesian Optimization with Frequency Modulated Kernels

The sample efficiency of Bayesian optimization(BO) is often boosted by Gaussian Process(GP) surrogate models. However, on mixed variable spaces, surrogate models other than GPs are prevalent, mainly due to the lack of kernels which can model complex dependencies across different types of variables. In this paper, we propose the frequency modulated (FM) kernel flexibly modeling dependencies among different types of variables, so that BO can enjoy the further improved sample efficiency. The FM kernel uses distances on continuous variables to modulate the graph Fourier spectrum derived from discrete variables. However, the frequency modulation does not always define a kernel with the similarity measure behavior which returns higher values for pairs of more similar points. Therefore, we specify and prove conditions for FM kernels to be positive definite and to exhibit the similarity measure behavior. In experiments, we demonstrate the improved sample efficiency of GP BO using FM kernels (BO-FM).On synthetic problems and hyperparameter optimization problems, BO-FM outperforms competitors consistently. Also, the importance of the frequency modulation principle is empirically demonstrated on the same problems. On joint optimization of neural architectures and SGD hyperparameters, BO-FM outperforms competitors including Regularized evolution(RE) and BOHB. Remarkably, BO-FM performs better even than RE and BOHB using three times as many evaluations.

Radial and Directional Posteriors for Bayesian Neural Networks

We propose a new variational family for Bayesian neural networks. We decompose the variational posterior into two components, where the radial component captures the strength of each neuron in terms of its magnitude; while the directional component captures the statistical dependencies among the weight parameters. The dependencies learned via the directional density provide better modeling performance compared to the widely-used Gaussian mean-field-type variational family. In addition, the strength of input and output neurons learned via the radial density provides a structured way to compress neural networks. Indeed, experiments show that our variational family improves predictive performance and yields compressed networks simultaneously.

Combinatorial Bayesian Optimization using Graph Representations

This paper focuses on Bayesian Optimization - typically considered with continuous inputs - for discrete search input spaces, including integer, categorical or graph structured input variables. In Gaussian process-based Bayesian Optimization a problem arises, as it is not straightforward to define a proper kernel on discrete input structures, where no natural notion of smoothness or similarity could be provided. We propose COMBO, a method that represents values of discrete variables as vertices of a graph and then use the diffusion kernel on that graph. As the graph size explodes with the number of categorical variables and categories, we propose the graph Cartesian product to decompose the graph into smaller sub-graphs, enabling kernel computation in linear time with respect to the number of input variables. Moreover, in our formulation we learn a scale parameter per subgraph. In empirical studies on four discrete optimization problems we demonstrate that our method is on par or outperforms the state-of-the-art in discrete Bayesian optimization.