When Redundancy Matters: Machine Teaching of Representations

In traditional machine teaching, a teacher wants to teach a concept to a learner, by means of a finite set of examples, the witness set. But concepts can have many equivalent representations. This redundancy strongly affects the search space, to the extent that teacher and learner may not be able to easily determine the equivalence class of each representation. In this common situation, instead of teaching concepts, we explore the idea of teaching representations. We work with several teaching schemas that exploit representation and witness size (Eager, Greedy and Optimal) and analyze the gains in teaching effectiveness for some representational languages (DNF expressions and Turing-complete P3 programs). Our theoretical and experimental results indicate that there are various types of redundancy, handled better by the Greedy schema introduced here than by the Eager schema, although both can be arbitrarily far away from the Optimal. For P3 programs we found that witness sets are usually smaller than the programs they identify, which is an illuminating justification of why machine teaching from examples makes sense at all.

Predictable Artificial Intelligence

We introduce the fundamental ideas and challenges of Predictable AI, a nascent research area that explores the ways in which we can anticipate key indicators of present and future AI ecosystems. We argue that achieving predictability is crucial for fostering trust, liability, control, alignment and safety of AI ecosystems, and thus should be prioritised over performance. While distinctive from other areas of technical and non-technical AI research, the questions, hypotheses and challenges relevant to Predictable AI were yet to be clearly described. This paper aims to elucidate them, calls for identifying paths towards AI predictability and outlines the potential impact of this emergent field.

Fairness and Missing Values

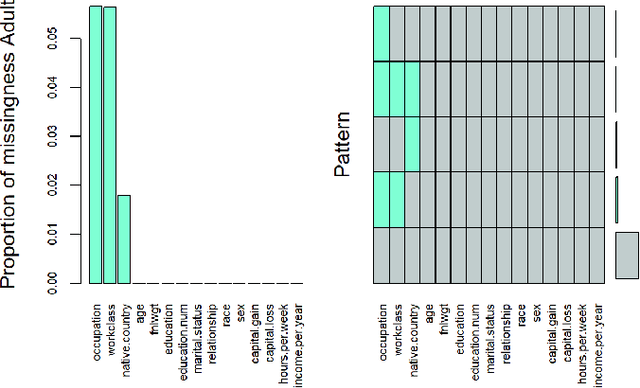
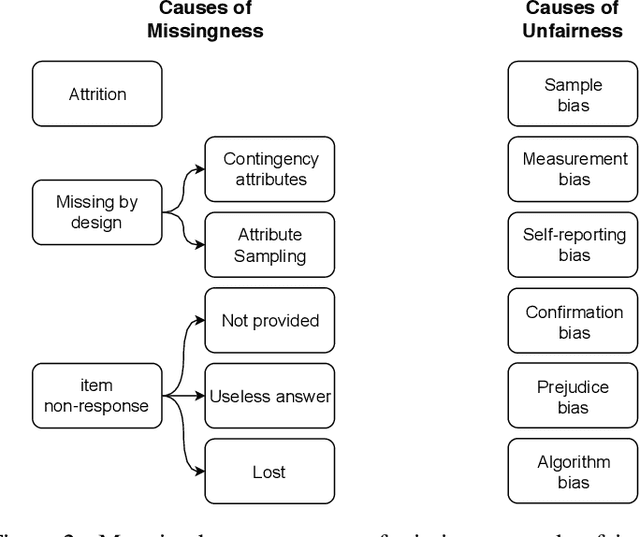
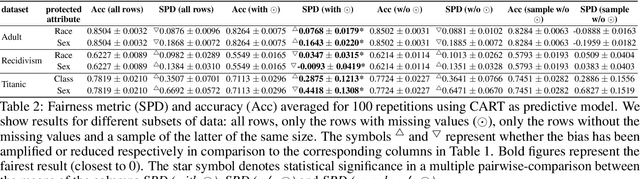
The causes underlying unfair decision making are complex, being internalised in different ways by decision makers, other actors dealing with data and models, and ultimately by the individuals being affected by these decisions. One frequent manifestation of all these latent causes arises in the form of missing values: protected groups are more reluctant to give information that could be used against them, delicate information for some groups can be erased by human operators, or data acquisition may simply be less complete and systematic for minority groups. As a result, missing values and bias in data are two phenomena that are tightly coupled. However, most recent techniques, libraries and experimental results dealing with fairness in machine learning have simply ignored missing data. In this paper, we claim that fairness research should not miss the opportunity to deal properly with missing data. To support this claim, (1) we analyse the sources of missing data and bias, and we map the common causes, (2) we find that rows containing missing values are usually fairer than the rest, which should not be treated as the uncomfortable ugly data that different techniques and libraries get rid of at the first occasion, and (3) we study the trade-off between performance and fairness when the rows with missing values are used (either because the technique deals with them directly or by imputation methods). We end the paper with a series of recommended procedures about what to do with missing data when aiming for fair decision making.

Forgetting and consolidation for incremental and cumulative knowledge acquisition systems

The application of cognitive mechanisms to support knowledge acquisition is, from our point of view, crucial for making the resulting models coherent, efficient, credible, easy to use and understandable. In particular, there are two characteristic features of intelligence that are essential for knowledge development: forgetting and consolidation. Both plays an important role in knowledge bases and learning systems to avoid possible information overflow and redundancy, and in order to preserve and strengthen important or frequently used rules and remove (or forget) useless ones. We present an incremental, long-life view of knowledge acquisition which tries to improve task after task by determining what to keep, what to consolidate and what to forget, overcoming The Stability-Plasticity dilemma. In order to do that, we rate rules by introducing several metrics through the first adaptation, to our knowledge, of the Minimum Message Length (MML) principle to a coverage graph, a hierarchical assessment structure which treats evidence and rules in a unified way. The metrics are not only used to forget some of the worst rules, but also to set a consolidation process to promote those selected rules to the knowledge base, which is also mirrored by a demotion system. We evaluate the framework with a series of tasks in a chess rule learning domain.

On the definition of a general learning system with user-defined operators

In this paper, we push forward the idea of machine learning systems whose operators can be modified and fine-tuned for each problem. This allows us to propose a learning paradigm where users can write (or adapt) their operators, according to the problem, data representation and the way the information should be navigated. To achieve this goal, data instances, background knowledge, rules, programs and operators are all written in the same functional language, Erlang. Since changing operators affect how the search space needs to be explored, heuristics are learnt as a result of a decision process based on reinforcement learning where each action is defined as a choice of operator and rule. As a result, the architecture can be seen as a 'system for writing machine learning systems' or to explore new operators where the policy reuse (as a kind of transfer learning) is allowed. States and actions are represented in a Q matrix which is actually a table, from which a supervised model is learnt. This makes it possible to have a more flexible mapping between old and new problems, since we work with an abstraction of rules and actions. We include some examples sharing reuse and the application of the system gErl to IQ problems. In order to evaluate gErl, we will test it against some structured problems: a selection of IQ test tasks and some experiments on some structured prediction problems (list patterns).

Threshold Choice Methods: the Missing Link

Many performance metrics have been introduced for the evaluation of classification performance, with different origins and niches of application: accuracy, macro-accuracy, area under the ROC curve, the ROC convex hull, the absolute error, and the Brier score (with its decomposition into refinement and calibration). One way of understanding the relation among some of these metrics is the use of variable operating conditions (either in the form of misclassification costs or class proportions). Thus, a metric may correspond to some expected loss over a range of operating conditions. One dimension for the analysis has been precisely the distribution we take for this range of operating conditions, leading to some important connections in the area of proper scoring rules. However, we show that there is another dimension which has not received attention in the analysis of performance metrics. This new dimension is given by the decision rule, which is typically implemented as a threshold choice method when using scoring models. In this paper, we explore many old and new threshold choice methods: fixed, score-uniform, score-driven, rate-driven and optimal, among others. By calculating the loss of these methods for a uniform range of operating conditions we get the 0-1 loss, the absolute error, the Brier score (mean squared error), the AUC and the refinement loss respectively. This provides a comprehensive view of performance metrics as well as a systematic approach to loss minimisation, namely: take a model, apply several threshold choice methods consistent with the information which is (and will be) available about the operating condition, and compare their expected losses. In order to assist in this procedure we also derive several connections between the aforementioned performance metrics, and we highlight the role of calibration in choosing the threshold choice method.

Technical Note: Towards ROC Curves in Cost Space

ROC curves and cost curves are two popular ways of visualising classifier performance, finding appropriate thresholds according to the operating condition, and deriving useful aggregated measures such as the area under the ROC curve (AUC) or the area under the optimal cost curve. In this note we present some new findings and connections between ROC space and cost space, by using the expected loss over a range of operating conditions. In particular, we show that ROC curves can be transferred to cost space by means of a very natural way of understanding how thresholds should be chosen, by selecting the threshold such that the proportion of positive predictions equals the operating condition (either in the form of cost proportion or skew). We call these new curves {ROC Cost Curves}, and we demonstrate that the expected loss as measured by the area under these curves is linearly related to AUC. This opens up a series of new possibilities and clarifies the notion of cost curve and its relation to ROC analysis. In addition, we show that for a classifier that assigns the scores in an evenly-spaced way, these curves are equal to the Brier Curves. As a result, this establishes the first clear connection between AUC and the Brier score.