Dynamics of Serial Manipulators using Dual Quaternion Algebra

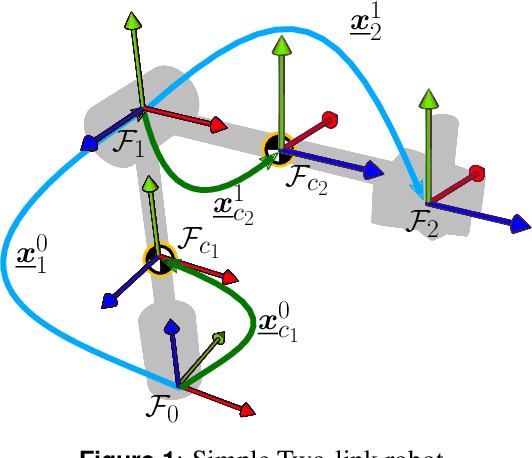
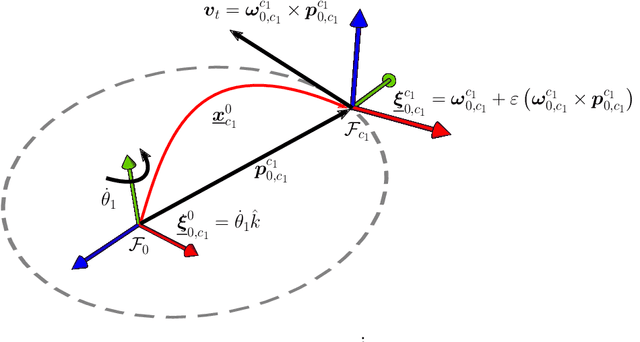
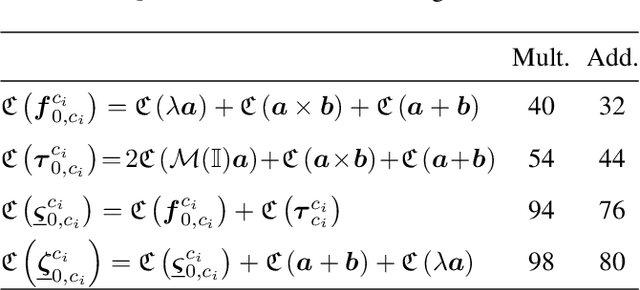
This paper presents two approaches to obtain the dynamical equations of serial manipulators using dual quaternion algebra. The first one is based on the recursive Newton-Euler formulation and uses twists and wrenches instead of 3D vectors, which simplifies the classic procedure by removing the necessity of exhaustive geometrical analyses since wrenches and twists are propagated through high-level algebraic operations. Furthermore, the proposed formulation works for arbitrary types of joints and does not impose any particular convention for the propagation of twists. The second approach, based on Gauss's Principle of Least Constraint (GPLC), takes into account elements of the dual quaternion algebra and provides a linear relationship between twists derivatives and joint accelerations, which can be particularly useful in robot control. Differently from other approaches based on the GPLC, which have representational singularities or require constraints, our method does not have those drawbacks. We present a thorough methodology to obtain the computational cost of both algorithms and compared them with their classic counterparts. Although our current formulations are more computationally expensive, they are more general than their counterparts in the state of the art. Simulation results showed that both methods are as accurate as the classic recursive Newton-Euler algorithm.

A Unified Framework for the Teleoperation of Surgical Robots in Constrained Workspaces

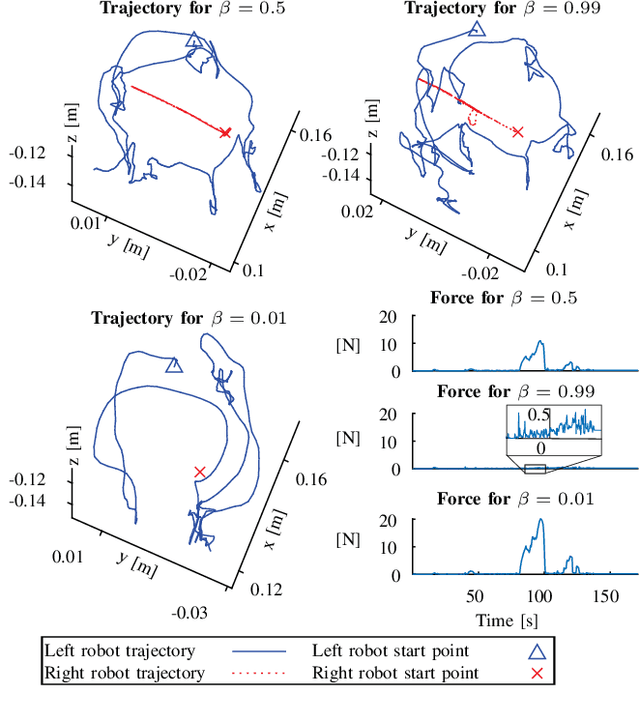
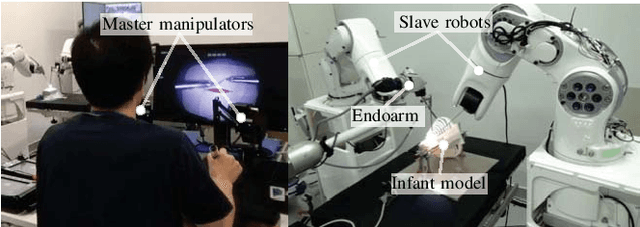
In adult laparoscopy, robot-aided surgery is a reality in thousands of operating rooms worldwide, owing to the increased dexterity provided by the robotic tools. Many robots and robot control techniques have been developed to aid in more challenging scenarios, such as pediatric surgery and microsurgery. However, the prevalence of case-specific solutions, particularly those focused on non-redundant robots, reduces the reproducibility of the initial results in more challenging scenarios. In this paper, we propose a general framework for the control of surgical robotics in constrained workspaces under teleoperation, regardless of the robot geometry. Our technique is divided into a slave-side constrained optimization algorithm, which provides virtual fixtures, and with Cartesian impedance on the master side to provide force feedback. Experiments with two robotic systems, one redundant and one non-redundant, show that smooth teleoperation can be achieved in adult laparoscopy and infant surgery.

Dynamic Active Constraints for Surgical Robots using Vector Field Inequalities

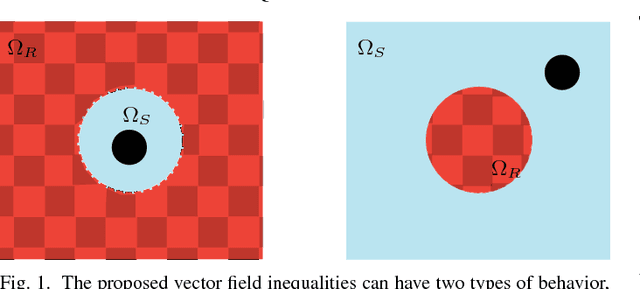
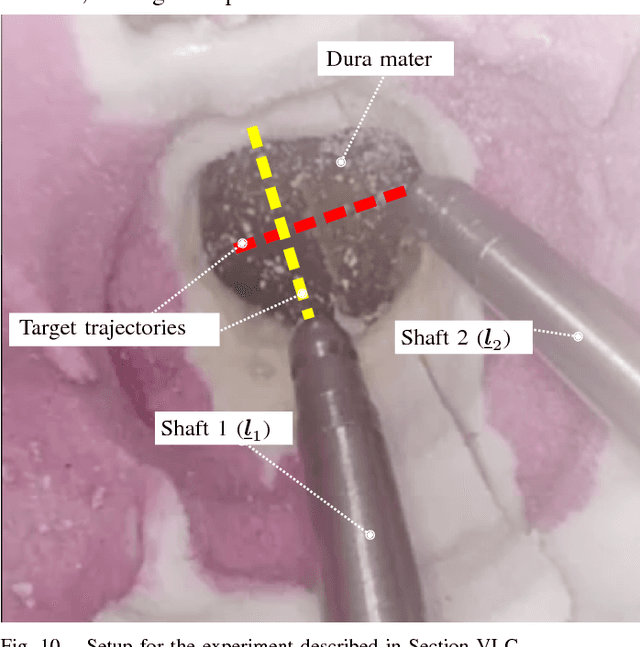
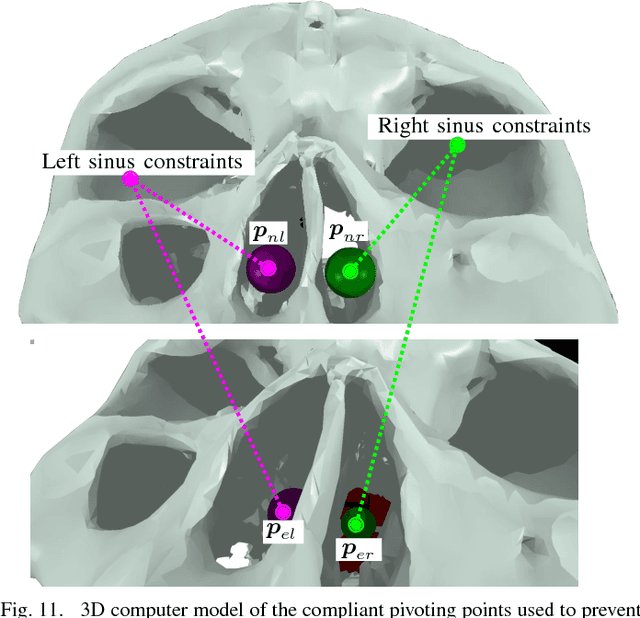
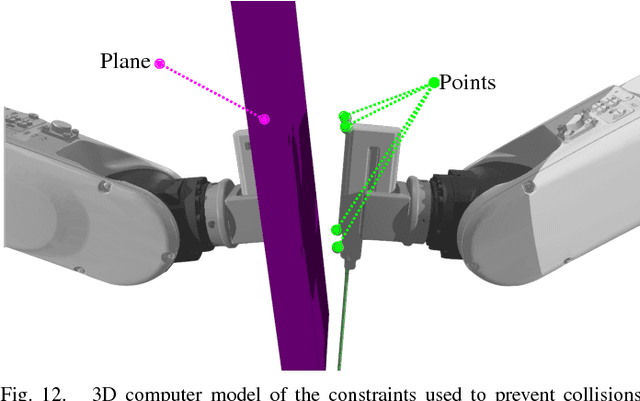
Robotic assistance allows surgeons to perform dexterous and tremor-free procedures, but robotic aid is still underrepresented in procedures with constrained workspaces, such as deep brain neurosurgery and endonasal surgery. In these procedures, surgeons have restricted vision to areas near the surgical tooltips, which increases the risk of unexpected collisions between the shafts of the instruments and their surroundings. In this work, our vector-field-inequalities method is extended to provide dynamic active-constraints to any number of robots and moving objects sharing the same workspace. The method is evaluated with experiments and simulations in which robot tools have to avoid collisions autonomously and in real-time, in a constrained endonasal surgical environment. Simulations show that with our method the combined trajectory error of two robotic systems is optimal. Experiments using a real robotic system show that the method can autonomously prevent collisions between the moving robots themselves and between the robots and the environment. Moreover, the framework is also successfully verified under teleoperation with tool-tissue interactions.

Pose consensus based on dual quaternion algebra with application to decentralized formation control of mobile manipulators

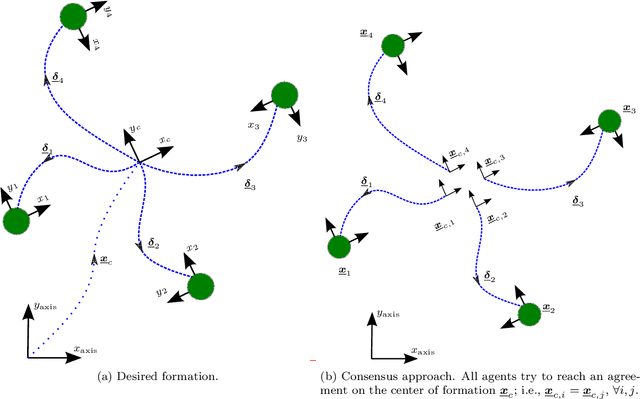
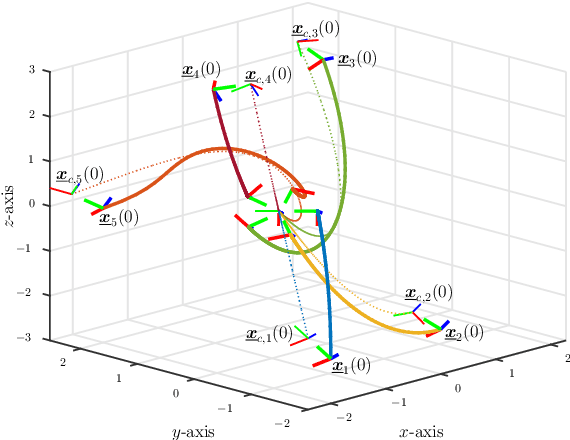
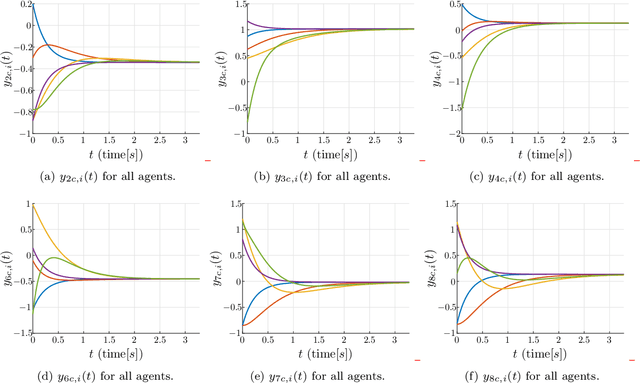
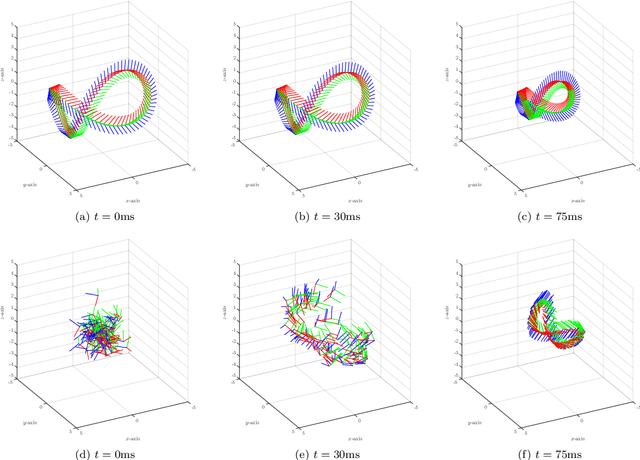
This paper presents a solution based on dual quaternion algebra to the general problem of pose (i.e., position and orientation) consensus for systems composed of multiple rigid-bodies. The dual quaternion algebra is used to model the agents' poses and also in the distributed control laws, making the proposed technique easily applicable to formation control of general robotic systems. The proposed pose consensus protocol has guaranteed convergence when the interaction among the agents is represented by directed graphs with directed spanning trees, which is a more general result when compared to the literature on formation control. In order to illustrate the proposed pose consensus protocol and its extension to the problem of formation control, we present a numerical simulation with a large number of free-flying agents and also an application of cooperative manipulation by using real mobile manipulators.

Active Constraints using Vector Field Inequalities for Surgical Robots

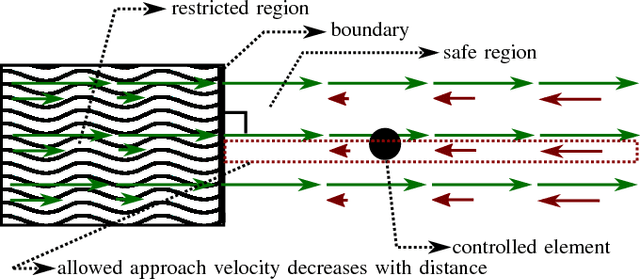
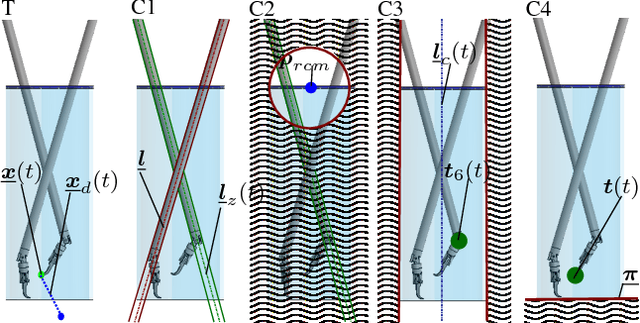
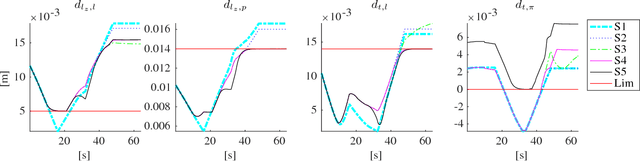
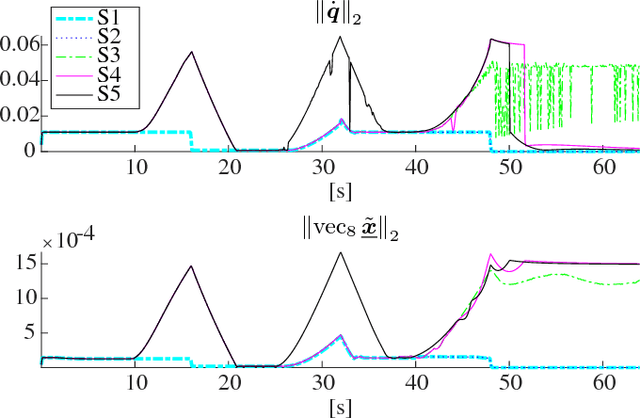
Robotic assistance allows surgeons to perform dexterous and tremor-free procedures, but is still underrepresented in deep brain neurosurgery and endonasal surgery where the workspace is constrained. In these conditions, the vision of surgeons is restricted to areas near the surgical tool tips, which increases the risk of unexpected collisions between the shafts of the instruments and their surroundings, in particular in areas outside the surgical field-of-view. Active constraints can be used to prevent the tools from entering restricted zones and thus avoid collisions. In this paper, a vector field inequality is proposed that guarantees that tools do not enter restricted zones. Moreover, in contrast with early techniques, the proposed method limits the tool approach velocity in the direction of the forbidden zone boundary, guaranteeing a smooth behavior and that tangential velocities will not be disturbed. The proposed method is evaluated in simulations featuring two eight degrees-of-freedom manipulators that were custom-designed for deep neurosurgery. The results show that both manipulator-manipulator and manipulator-boundary collisions can be avoided using the vector field inequalities.