Dynamics of Serial Manipulators using Dual Quaternion Algebra
Paper and Code
Jul 16, 2020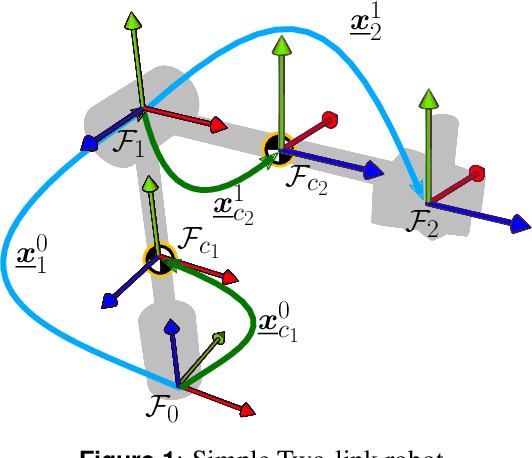

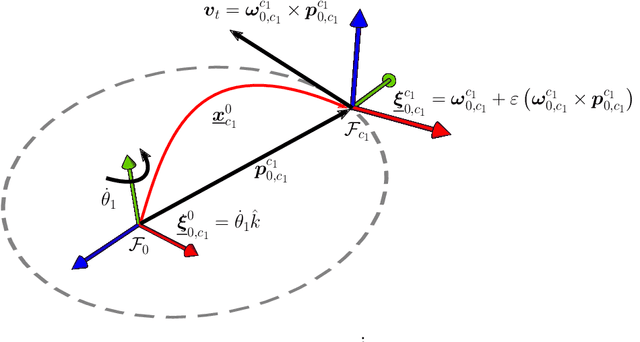
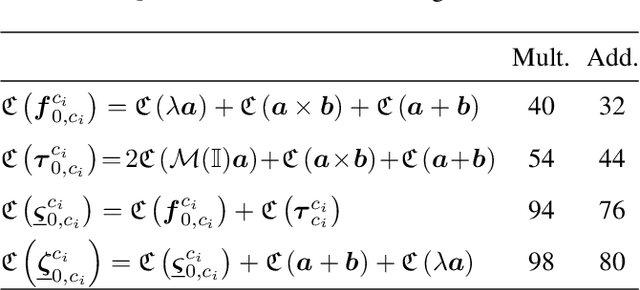
This paper presents two approaches to obtain the dynamical equations of serial manipulators using dual quaternion algebra. The first one is based on the recursive Newton-Euler formulation and uses twists and wrenches instead of 3D vectors, which simplifies the classic procedure by removing the necessity of exhaustive geometrical analyses since wrenches and twists are propagated through high-level algebraic operations. Furthermore, the proposed formulation works for arbitrary types of joints and does not impose any particular convention for the propagation of twists. The second approach, based on Gauss's Principle of Least Constraint (GPLC), takes into account elements of the dual quaternion algebra and provides a linear relationship between twists derivatives and joint accelerations, which can be particularly useful in robot control. Differently from other approaches based on the GPLC, which have representational singularities or require constraints, our method does not have those drawbacks. We present a thorough methodology to obtain the computational cost of both algorithms and compared them with their classic counterparts. Although our current formulations are more computationally expensive, they are more general than their counterparts in the state of the art. Simulation results showed that both methods are as accurate as the classic recursive Newton-Euler algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge